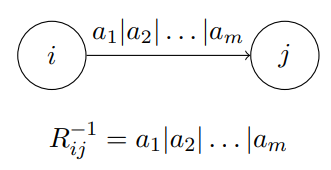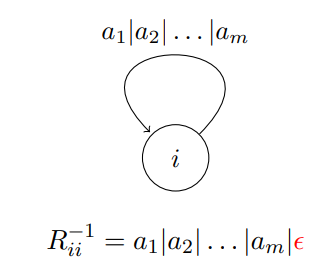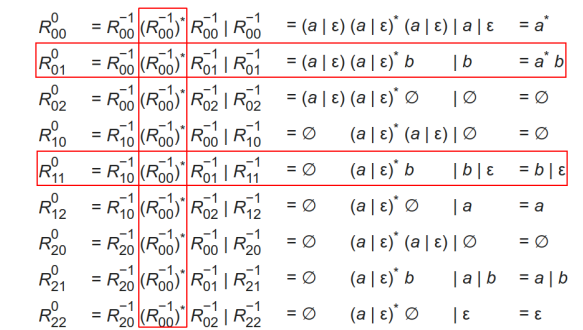编译原理(2) 词法分析
2023-08-09 14:53:19 # NJU # 编译原理

词法分析

一、词法分析器生成器 ANTLR v4

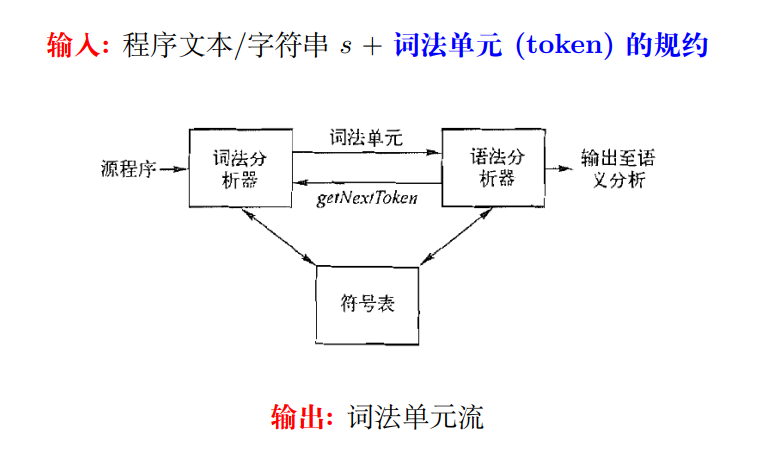
1. 输入与输出

image-20221108235621687

2. 词法分析器的三种设计方法

由易到难

  • 词法分析器生成器:ANTLR

    • 输入规约(.g4)，自动生成词法分析器(lexer.java)
    • src —> lexer —> string of tokens

  • 手写词法分析器

  • 自动化词法分析器

生产环境下的编译器 (如 gcc) 通常选择手写词法分析器

3. ANTLR4

3.1 输入与输出

image-20221108235911855

3.2 冲突解决规则

ANTLR v4 中两大冲突解决规则

  • 最前优先匹配: 关键字 vs. 标识符
  • 最长优先匹配: >=, ifhappy, thenext, 1.23

3.3 词法单元的规约

image-20221109000228279

我们需要词法单元的形式化规约

id: 字母开头的字母/数字串

id 定义了一个集合, 我们称之为语言 (Language)

它使用了字母与数字等符号集合, 我们称之为字母表 (Alphabet)

该语言中的每个元素 (即, 标识符) 称为串 (String)

Definition (字母表)

字母表 $\Sigma$ 是一个有限的符号集合。

image-20221109000640673

Definition (串)

字母表 $\Sigma$ 上的串 ($s$) 是由 $\Sigma$ 中符号构成的一个有穷序列。

image-20221109000729588

Definition (串上的 “连接” 运算)

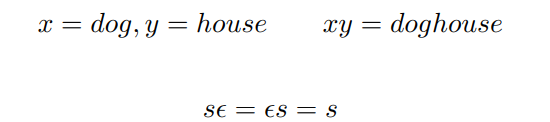
image-20221109000814846

Definition (串上的 “指数” 运算)

也是连接

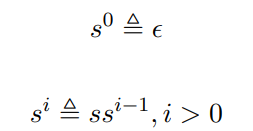
image-20221109000844290

Definition (语言)

语言是给定字母表 $\Sigma$ 上一个任意的可数的串集合。

image-20221109160847077

语言是串的集合

因此, 我们可以通过集合操作构造新的语言。

3.4 语言的集合操作

image-20221109161009360

$L^* = (L^0) ∪ (L^1) ∪ (L^2) ∪ (L^3)$…

$L^+ = (L^1) ∪ (L^2) ∪ (L^3)$…

image-20221109161535054

image-20221115163150026

image-20221109161603205

3.5 正则表达式

image-20221109153140556

Definition (正则表达式)

image-20221109153528379

Definition (正则表达式对应的正则语言)

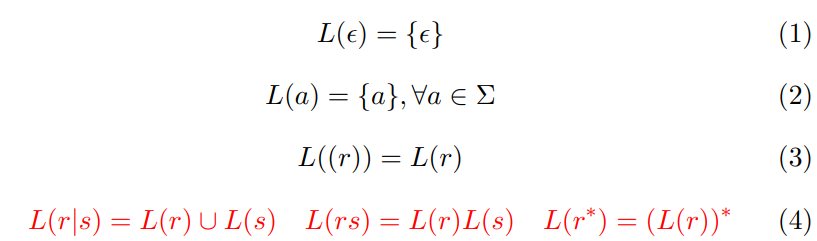
image-20221109163520214

举例

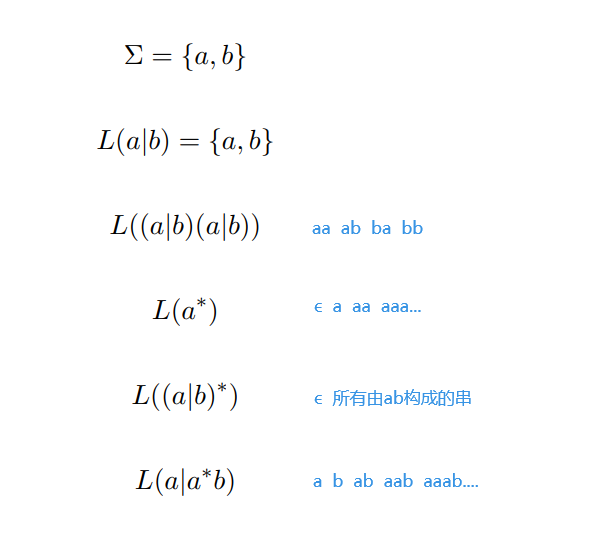
image-20221109163813902

正则语法

image-20221109170417873

antlr中 . 可以匹配换行

antlr中使用~[abc]而不是[^abc]

注意转义

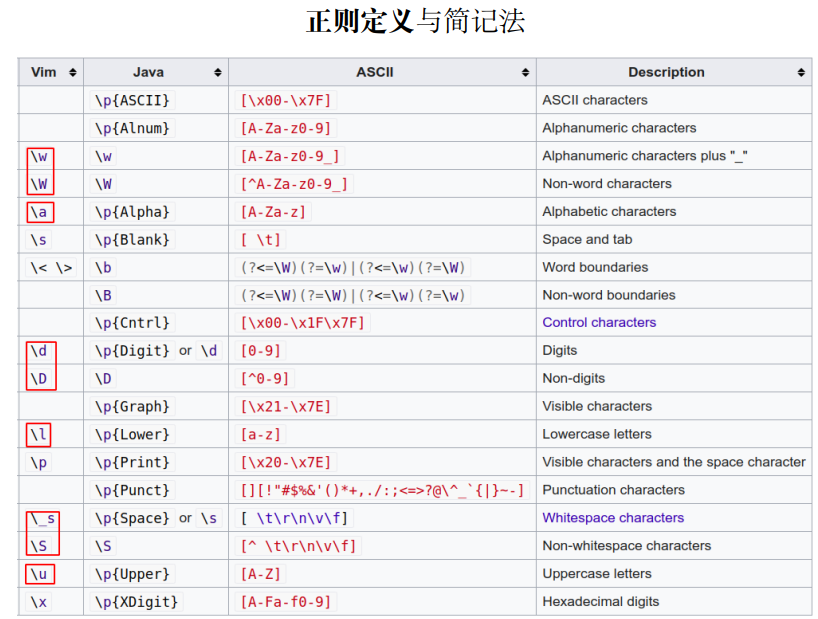
image-20221109170509879

$(0|(1(01^*0)^∗1))^∗$ 匹配所有3的倍数(二进制表示)

https://regex101.com/r/ED4qgC/1

二、手写词法分析器

代码见：https://github.com/courses-at-nju-by-hfwei/2022-compilers-coding

image-20221115165313782

1. 分支与循环

image-20221115171159071

// 遍历所有Token
Token token = lexer.nextToken();
while (token != Token.EOF) {
    if (token != Token.WS) {
        System.out.println(token);
    }
    token = lexer.nextToken();
}

2. 状态转移图

2.1 用于识别 ws 的状态转移图

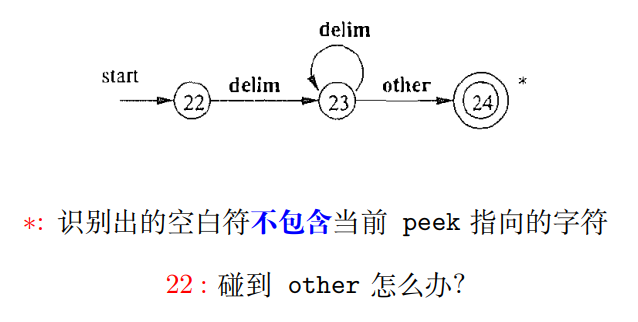
image-20221115172525171

// 后面的示例省略nextToken中的分支代码
public Token nextToken() {
	if (Character.isWhitespace(peek)) {
      	return WS();
    }
}
private Token WS() {
    while (Character.isWhitespace(peek)) {
      	advance();
    }
    return Token.WS;
}

2.2 用于识别 id 的状态转移图

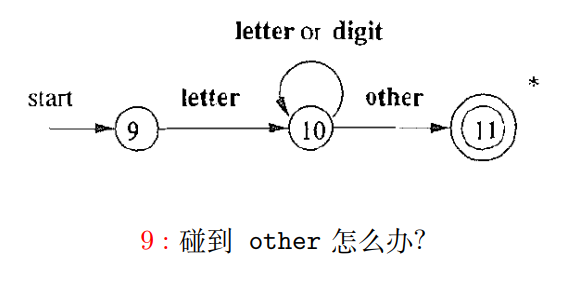
image-20221115172813225

private Token ID() {
    StringBuilder sb = new StringBuilder();
    do {
      	sb.append(peek);
      	advance();
    } while (Character.isLetterOrDigit(peek));
	// 判断是不是保留字
    Token token = this.kwTable.getKeyword(sb.toString());
    if (token == null) {
      	return new Token(TokenType.ID, sb.toString());
    }
    return token;
}

2.3 用于识别 int 的状态转移图

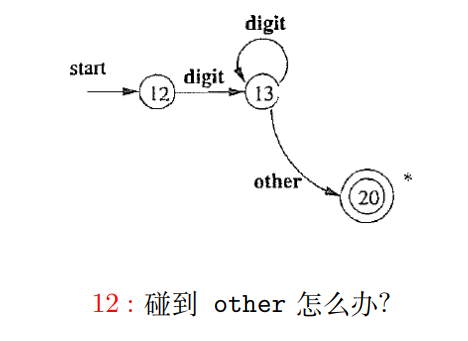
image-20221115173217304

private Token INT() {
    StringBuilder sb = new StringBuilder();
    do {
      	sb.append(peek);
     	advance();
    } while (Character.isDigit(peek));

    return new Token(TokenType.INT, sb.toString());
}

2.4 用于识别 relop 的状态转移图

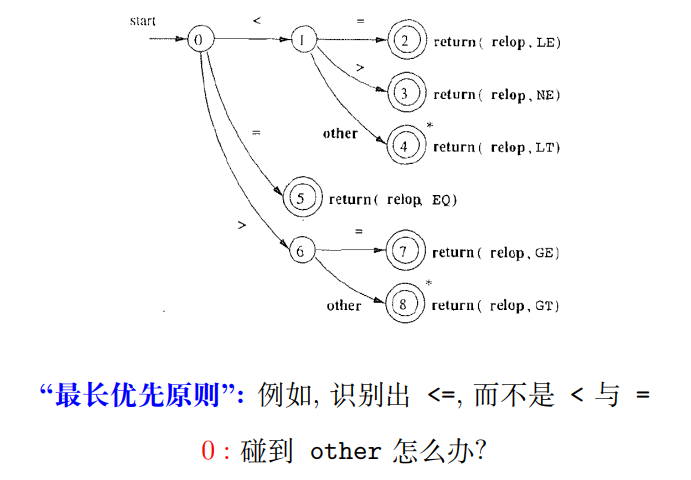
image-20221115173556563

if (peek == '=') {
  	advance();
  	return Token.EQ;
}

if (peek == '>') {
  	advance();
  	if (peek == '=') {
    	advance();
    	return Token.GE;
  	}
  	return Token.GT;
}

if (peek == '<') {
  	advance();
  	if (peek == '=') {
    	advance();
    	return Token.LE;
  	}
  	if (peek == '>') {
    	advance();
    	return Token.NE;
  	}
  	return Token.GT;
}

2.5 错误处理

识别字符串 $s$ 中符合某种词法单元模式的前缀词素(nextToken())

关键点：合并 22, 12, 9, 0, 根据下一个字符即可判定词法单元的类型。否则, 调用错误处理模块(对应 other), 报告该字符有误, 并忽略该字符

// unknown tokens (characters)
Token unknown = new Token(TokenType.UNKNOWN, Character.toString(peek));
advance();
return unknown;

image-20221115173952384

2.6 用于识别 num 的状态转移图

2.6.1 分为三个部分

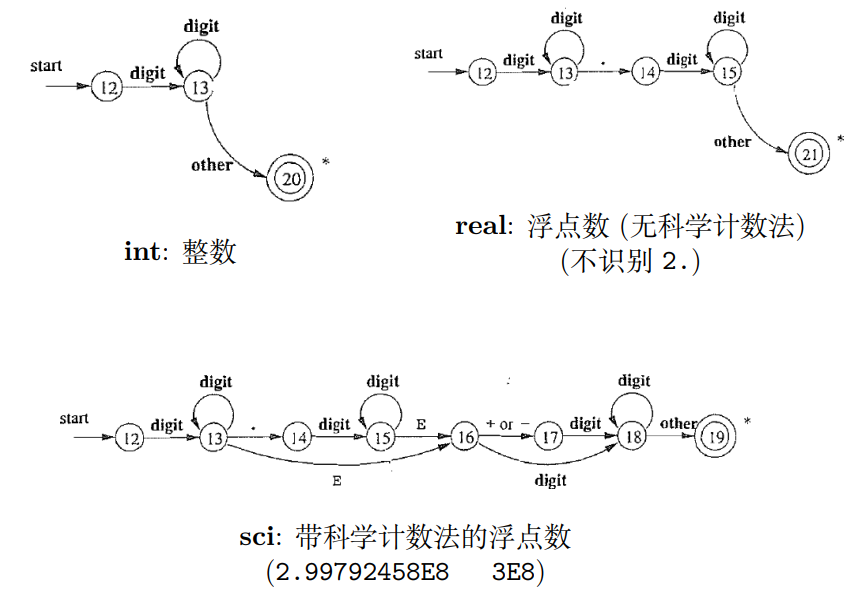
image-20221115174022886

2.6.2 完整

num: 整数部分[. 可选的小数部分][E[可选的 +-] 可选的指数部分]

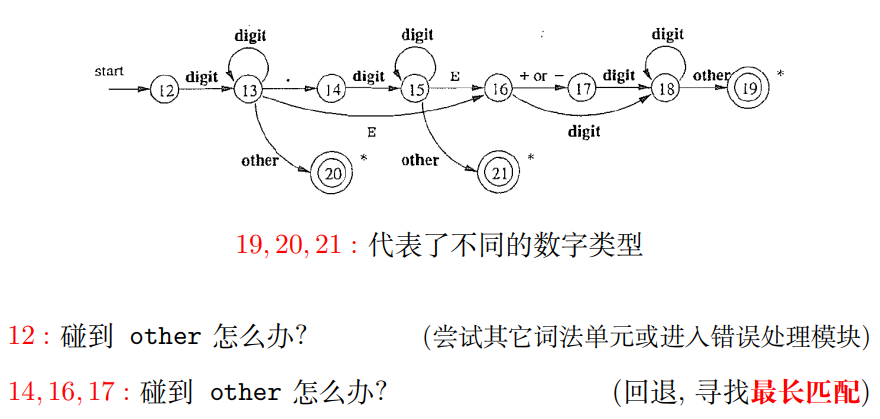
image-20221115174225767

关键点: 合并 22, 12, 9, 0, 根据下一个字符即可判定词法单元的类型。否则, 调用错误处理模块 (对应 other), 报告该字符有误, 忽略该字符。

注意, 在 real 与 sci 中, 有时需要回退, 寻找最长匹配。

private Token NUMBER() {
    StringBuilder intStr = new StringBuilder();
    intStr.append(peek);
    advance();

    int intPos = -1;
    int realPos = -1;

    StringBuilder realStr = new StringBuilder();
    StringBuilder sciStr = new StringBuilder();

    int state = 13;
    while (true) {
        switch (state) {
            case 13:
                intPos = pos;
                if (Character.isDigit(peek)) {
                    intStr.append(peek);
                    advance();
                    state = 13;
                    break;
                } else if (peek == '.') {
                    realStr.append(peek);
                    advance();
                    state = 14;
                    break;
                } else if (peek == 'E' || peek == 'e') {
                    sciStr.append(peek);
                    advance();
                    state = 16;
                    break;
                } else {
                    return new Token(TokenType.INT, intStr.toString());
                }
            case 14:
                if (Character.isDigit(peek)) {
                    realStr.append(peek);
                    advance();
                    state = 15;
                    break;
                } else {
                    this.reset(intPos);
                    return new Token(TokenType.INT, intStr.toString());
                }
            case 15:
                realPos = pos;
                if (Character.isDigit(peek)) {
                    realStr.append(peek);
                    advance();
                    state = 15;
                    break;
                } else if (peek == 'E' || peek == 'e') 
                    sciStr.append(peek);
                    advance();
                    state = 16;
                    break;
                } else {
                    return new Token(TokenType.REAL, intStr.append(realStr).toString());
                }
            case 16:
                if (peek == '+' || peek == '-') {
                    sciStr.append(peek);
                    advance();
                    state = 17;
                    break;
                } else if (Character.isDigit(peek)) {
                    sciStr.append(peek);
                    advance();
                    state = 18;
                    break;
                } else {
                    this.reset(realPos);
                    return new Token(TokenType.REAL, intStr.append(realStr).toString());
                }
            case 17:
                if (Character.isDigit(peek)) {
                    sciStr.append(peek);
                    advance();
                    state = 18;
                    break;
                } else {
                    this.reset(realPos);
                    return new Token(TokenType.REAL, intStr.append(realStr).toString());
                }
            case 18:
                if (Character.isDigit(peek)) {
                    sciStr.append(peek);
                    advance();
                    state = 18;
                    break;
                } else {
                    return new Token(TokenType.SCI, intStr.append(realStr).append(sciStr).toString());
                }
            default:
                System.err.println("Unreachable");
        }
    }
}

三、自动机理论与词法分析器生成器

1. 自动机

(Automaton 单数; Automata 复数)

image-20221115231221748

  • 两大要素：状态集 $S$ 以及状态转移函数 $\delta$

  • 根据表达/计算能力的强弱, 自动机可以分为不同层次

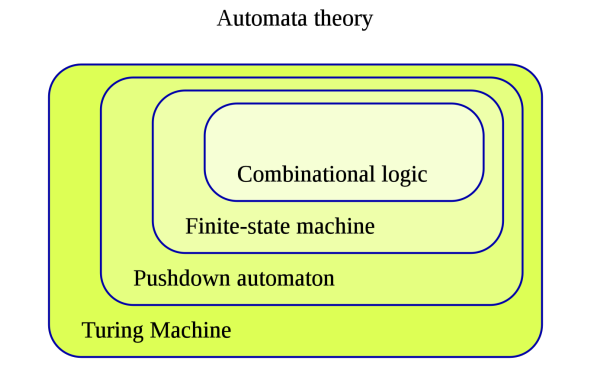
image-20221115231515551

2. 目标：正则表达式 RE ==> 词法分析器

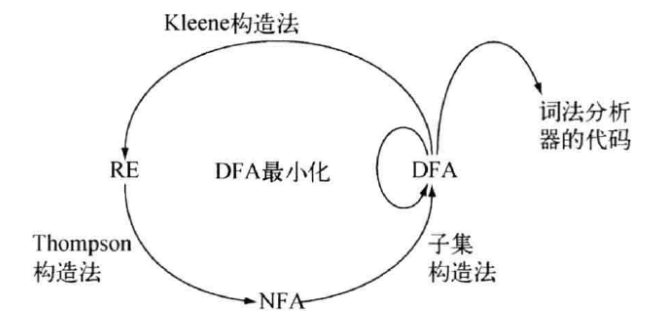
image-20221115231625992

终点固然令人向往, 这一路上的风景更是美不胜收

2.1 Definition (NFA (Nondeterministic Finite Automaton))

  • 非确定性有穷自动机 $\mathcal{A}$ 是一个五元组 $\textcolor{red}{\mathcal{A} = (\Sigma, S, s_0, \delta, F)}$:

    1. 字母表 $\Sigma (\epsilon \notin \Sigma)$

    2. 有穷的状态集合 $S$

    3. 唯一的初始状态 $s_0 \in S$

    4. 状态转移函数 $\delta$

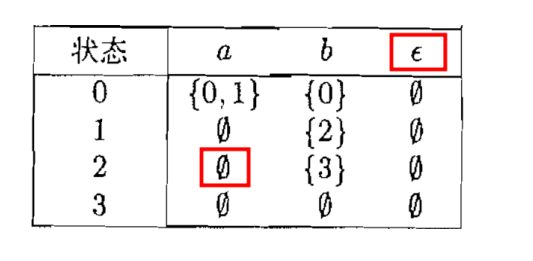
      $\delta: S \times (\Sigma \cup \{ \textcolor{blue}{\epsilon} \}) \rightarrow \textcolor{blue}{2^S} $

    5. 接受状态集合 $F \subseteq S$

image-20221115234212017

非确定性的来源：$\delta: S \times (\Sigma \cup \{ \textcolor{blue}{\epsilon} \}) \rightarrow \textcolor{blue}{2^S} $

  • $\epsilon$: 没有新来的字符也可能转移状态

  • 接受同一个字符可能转移到不同的状态

$2^S$ 表示 $S$ 的所有子集, 包括空集

  • 约定：所有没有对应出边的字符默认指向一个不存在的 “空状态” $\emptyset$

image-20221115232743665

  • 提出

image-20221115232932323

“which introduced the idea of nondeterministic machines, which has proved to be an enormously valuable concept.”

  • (非确定性)有穷自动机是一类极其简单的计算装置
  • 它可以识别 (接受/拒绝) $\Sigma$ 上的字符串

2.2 Definition (接受 (Accept))

  • (非确定性)有穷自动机 $\mathcal{A}$ 接受字符串 $x$, 当且仅当存在一条从开始状态 $s_0$ 到某个接受状态 $f ∈ F$、标号为 $x$ 的路径。

  • 因此 $\mathcal{A}$ 定义了一种语言 $L(\mathcal{A})$: 它能接受的所有字符串构成的集合

    若该语言与某一 RE 定义的语言相等, 则表示该 RE 与该 NFA 等价

image-20221115234754835

2.3 关于自动机 $\mathcal{A}$ 的两个基本问题

image-20221115234935877

  • 例1

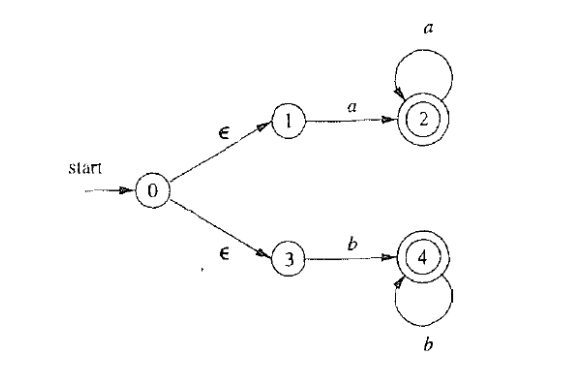
    image-20221115235112210

    • $aaa \in \mathcal{A}$: 接受

    • $aab \in \mathcal{A}$: 不接受

    • $\textcolor{red}{L(\mathcal{A})} = L((aa^{\ast} | bb^{\ast}))$

  • 例2

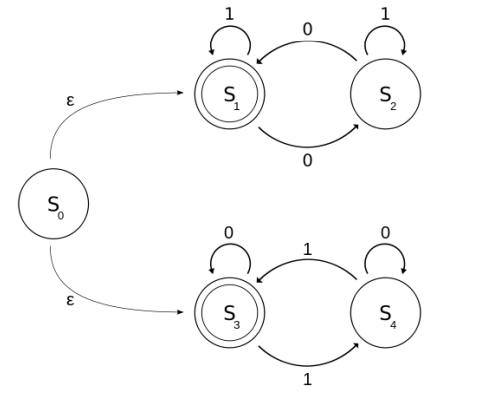
    image-20221115235502815

    • $1011 \in L(\mathcal{A})$: 不接受
    • $0011 \in L(\mathcal{A})$: 接受
    • $L(\mathcal{A}) = \{包含偶数个 1 或偶数个 0 的 01 串\}$

2.4 Definition (DFA (Deterministic Finite Automaton))

  • 确定性有穷自动机 $\mathcal{A}$ 是一个五元组 $\textcolor{red}{\mathcal{A} = (\Sigma, S, s_0, \delta, F)}$:

    1. 字母表 $\Sigma (\epsilon \notin \Sigma)$

    2. 有穷的状态集合 $S$

    3. 唯一的初始状态 $s_0 \in S$

    4. 状态转移函数 $\delta$

      $\delta: S \times \textcolor{blue}{\Sigma} \rightarrow \textcolor{blue}{S} $

    5. 接受状态集合 $F \subseteq S$

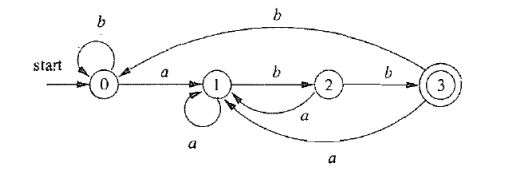
    image-20221116000025625

  • 约定: 所有没有对应出边的字符默认指向一个不存在的 “死状态”

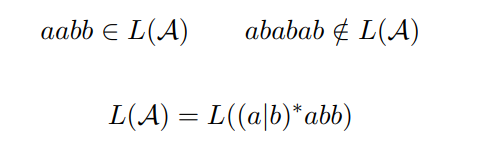
image-20221116000213842

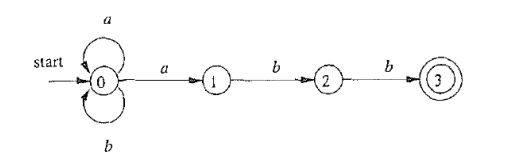
image-20221116000313618

上面的确定性自动机和非确定性自动机是等价的

2.5 归纳

  • NFA 简洁易于理解, 便于描述语言 $\textcolor{blue}{L(\mathcal{A})}$
  • DFA 易于判断 $\textcolor{blue}{x \in L(\mathcal{A})}$, 适合产生词法分析器
  • 用 NFA 描述语言, 用 DFA 实现词法分析器
  • $\textcolor{red}{RE \Rightarrow NFA \Rightarrow DFA \Rightarrow 词法分析器}$

image-20221115231625992

3. RE $\Rightarrow$ NFA

  • $r \Rightarrow N(r)$

  • 要求：$\textcolor{red}{L(N(r)) = L(r)}$

  • 从 RE 到 NFA: Thompson 构造法

    image-20221116142610957

  • Thompson 构造法的基本思想: 按结构归纳

3.1 Definition (正则表达式)

  • 给定字母表 $\Sigma$ , $\Sigma$ 上的正则表达式由且仅由以下规则定义:

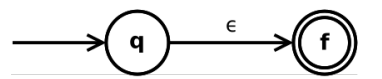
    1. $\epsilon$ 是正则表达式
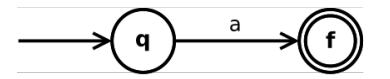
    2. $\forall a \in \Sigma$, $a$ 是正则表达式
    3. 如果 $s$ 是正则表达式, 则 $(s)$ 是正则表达式
    4. 如果 $s$ 和 $t$ 是正则表达式, 则 $s|t, st, s^{*}$ 也是正则表达式

  • $\epsilon$ 是正则表达式

    image-20221116144106907

  • $a \in \Sigma$ 是正则表达式

    image-20221116144202213

  • 如果 $s$ 是正则表达式, 则 $(s)$ 是正则表达式

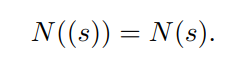
    image-20221116144239653

  • 如果 $s$, $t$ 是正则表达式, 则 $s|t$ 是正则表达式

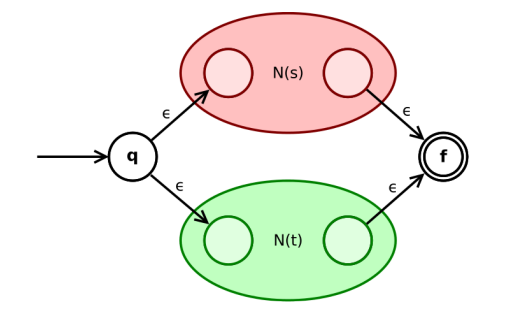
    image-20221116144408101

    • 如果 $N(s)$ 或 $N(t)$ 的开始状态或接受状态不唯一, 怎么办?
      • 根据归纳假设, $N(s)$ 与 $N(t)$ 的开始状态与接受状态均唯一

  • 如果 $s$, $t$ 是正则表达式, 则 $st$ 是正则表达式

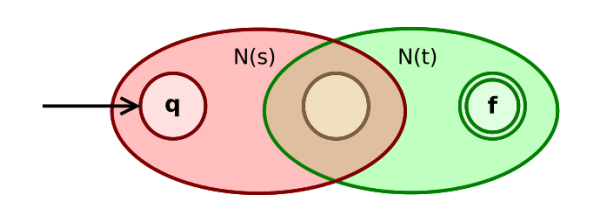
    image-20221116144528037

    • 根据归纳假设, $N(s)$ 与 $N(t)$ 的开始状态与接受状态均唯一

  • 如果 $s$ 是正则表达式, 则 $s^{*}$ 是正则表达式

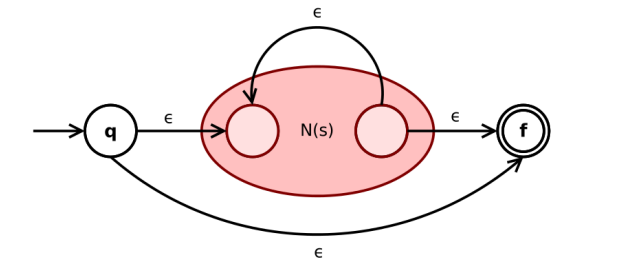
    image-20221116144724260

    • 根据归纳假设, $N(s)$ 的开始状态与接受状态均唯一

3.2 $N(r)$ 的性质以及 Thompson 构造法复杂度分析

  • $N(r)$ 的开始状态与接收状态均唯一

  • 开始状态没有入边, 接收状态没有出边

  • $N(r)$ 的状态数 $|S| \le 2 \times |r|$

    ($|r|: r$ 中运算符与运算分量的总和)

  • 每个状态最多有两个 $\epsilon$-入边与两个 $\epsilon$-出边

  • $\forall a \in \Sigma$, 每个状态最多有一个 $a$-入边与一个 $a$-出边

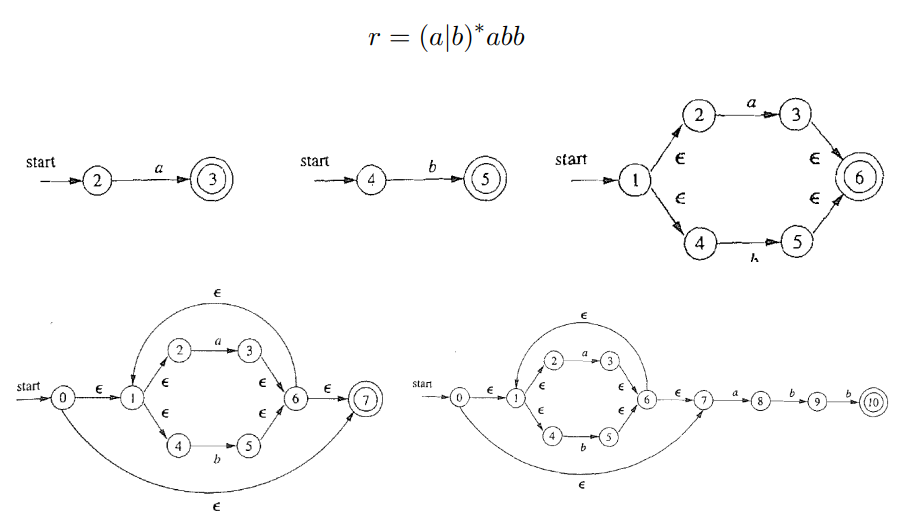
image-20221116165020990

4. NFA $\Rightarrow$ DFA

  • $N \Rightarrow D$

  • 要求: $\textcolor{red}{L(D) = L(N)}$

  • 从 NFA 到 DFA 的转换: 子集构造法(Subset/Powerset Construction)

    image-20221116165300828

  • 思想: 用 DFA 模拟 NFA

4.1 用 DFA 模拟 NFA

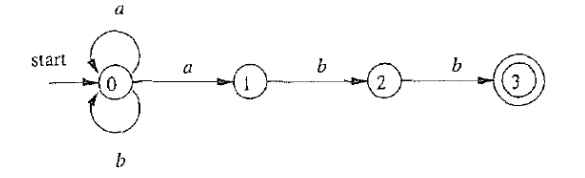
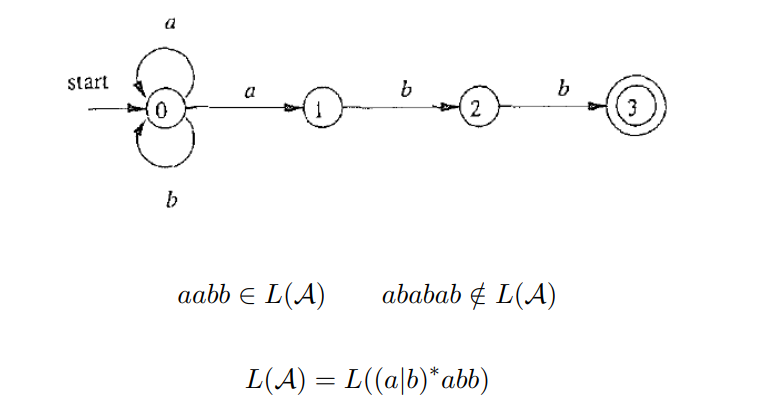
$\textcolor{blue}{L(\mathcal{A}) = L((a|b)^{*}abb)}$

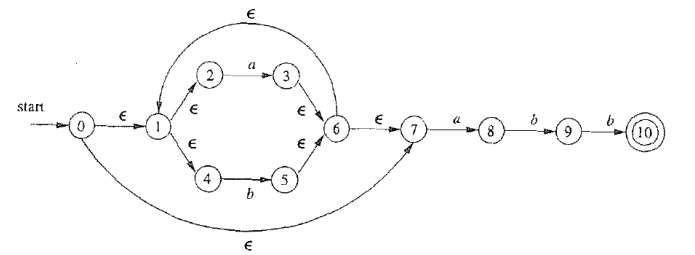
image-20221116170259111

  • 过程

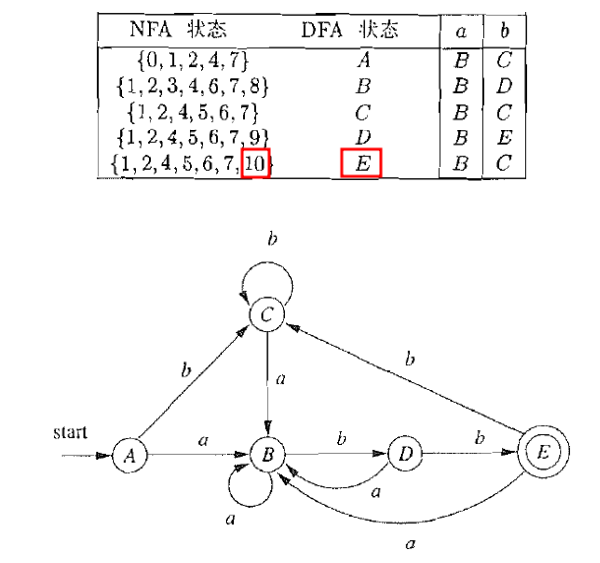
    image-20221116170337732

4.2 $\epsilon$-闭包

  • 从状态 $s$ 开始, 只通过 $\epsilon$-转移可达的状态集合

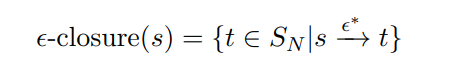
    image-20221116170523291

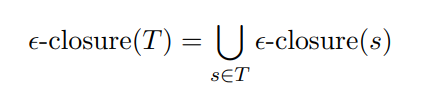
    image-20221116170532028

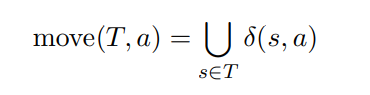
    image-20221116170546504

  • 闭包(Closure): $f$-closure($T$)

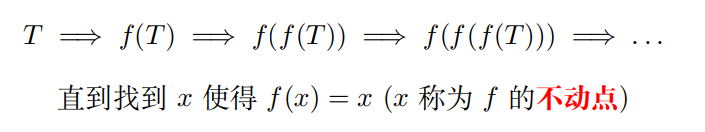
    image-20221116172358836

4.3 子集构造法($N \Rightarrow D$)的原理

image-20221116170833733

4.4 子集构造法的复杂度分析

$(|S_{N}| = n)$

  • $|S_{D}| = \Theta (2^{n})$

  • 最坏情况下, $|S_{D}| = \Omega (2^{n})$

  • 最坏情况举例

    • $L_{n} = (a|b)^{*}a(a|b)^{n-1}$

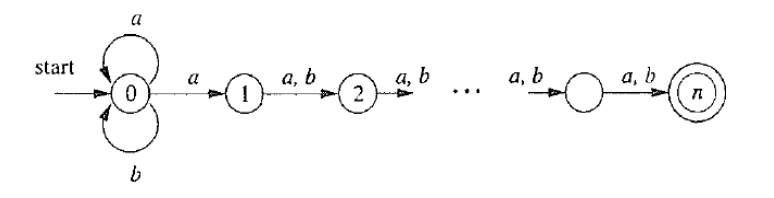
      image-20221116172141260

    • 当 n = 4

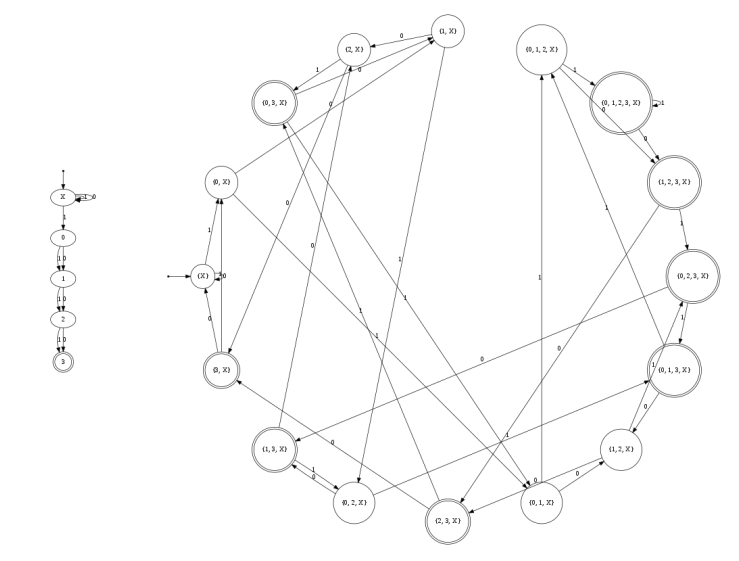
      image-20221116172204829

5. DFA 最小化

$\textcolor{blue}{L(\mathcal{A}) = L((a|b)^{*}abb)}$

  • 子集构造法得到的 DFA

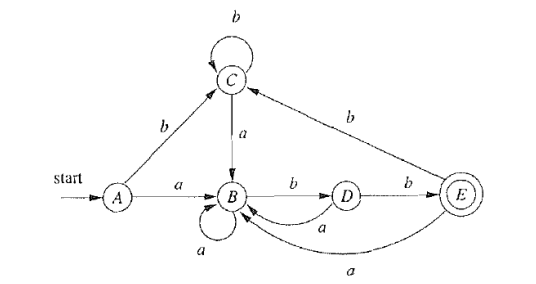
    image-20221116172537563

  • 最小化后的 DFA

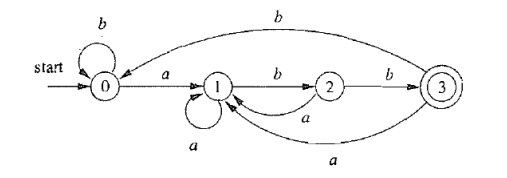
    image-20221116172557173

  • DFA 最小化算法基本思想: 等价的状态可以合并

    image-20221116172644918

    “With Robert E. Tarjan, for fundamental achievements in the design and analysis of algorithms and data structures” — Turing Award, 1986

5.1 如何定义等价状态

image-20221116220414892

image-20221116220456076

按照错误定义可得: $A \sim C \sim E$

但是, 接收状态与非接收状态必定不等价

空串 $\epsilon$ 区分了这两类状态

  • 正确定义：

    $s \sim t \iff \forall a \in \Sigma. \left((s \stackrel{a}{\rightarrow} s’) \land (t \stackrel{a}{\rightarrow} t’)\right) \implies (\textcolor{red}{s’ \sim t’})$

    $s \nsim t \iff \exists a \in \Sigma. (s \stackrel{a}{\rightarrow} s’) \land (t \stackrel{a}{\rightarrow} t’) \land (\textcolor{red}{s’ \nsim t’})$

5.2 合并 or 划分

5.2.1 合并

  • $s \sim t \iff \forall a \in \Sigma. \left((s \stackrel{a}{\rightarrow} s’) \land (t \stackrel{a}{\rightarrow} t’)\right) \implies (\textcolor{red}{s’ \sim t’})$

  • 基于该定义, 不断合并等价的状态, 直到无法合并为止

  • 但是, 这是一个递归定义, 从哪里开始呢

    Q: 所有的接收状态都是等价的吗？

    A: 当然不

    image-20221116225047710

  • 缺少基础情况, 不知从何下手

  • 划分, 而非合并
5.2.2 划分
  • $s \nsim t \iff \exists a \in \Sigma. (s \stackrel{a}{\rightarrow} s’) \land (t \stackrel{a}{\rightarrow} t’) \land (\textcolor{red}{s’ \nsim t’})$
    • 从哪里开始呢?
  • $\Pi = \set{F, S \setminus F}$
    • 接收状态与非接收状态必定不等价
    • 空串 $\epsilon$ 区分了这两类状态

Definition (字符串 $x$ 区分状态 $s$ 与 $t$)

  • 如果分别从 $s$ 与 $t$ 出发, 沿着标号为 $x$ 的路径到达的两个状态中只有一个是接受状态, 则称 $x$ 区分了状态 $s$ 与 $t$。

Definition (可区分的 (Distinguishable))

  • 如果存在某个能区分状态 $s$ 与 $t$ 的字符串, 则称 $s$ 与 $t$ 是可区分的。

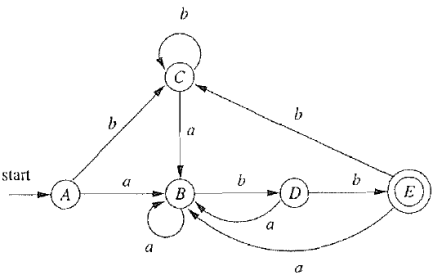
image-20221116230131399

  • 划分步骤

    image-20221117131345963

  • 合并等价状态 $A \sim C$

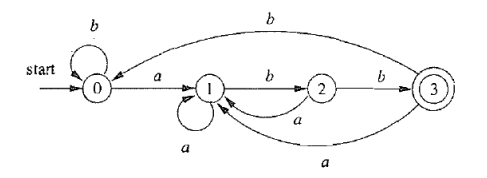
    image-20221116230509789

Q: 合并后是否一定还是 DFA? 初始状态、接受状态是哪些?

A: 是, 包含原来初始状态与接收状态的状态

5.3 算法总览

DFA 最小化等价状态划分方法

  • $\Pi = \set{F, S \setminus F}$

    image-20221116230748683

  • 直到再也无法划分为止 (不动点!)

  • 然后, 将同一等价类里的状态合并

注意

  • 这是 DFA 最小化算法, 要保证状态图完整
  • 要先检查是否需要补 “死状态” $\emptyset$

如何分析 DFA 最小化算法的复杂度?

为什么 DFA 最小化算法是正确的?

最小化 DFA 是唯一的吗?

DFA Minimization @ wiki

6. DFA $\Rightarrow$ 词法分析器

image-20221124164547540

  • 最前优先匹配: $abb$ (比如关键字)
  • 最长优先匹配: $aabbb$

6.1 根据正则表达式构造相应的 NFA

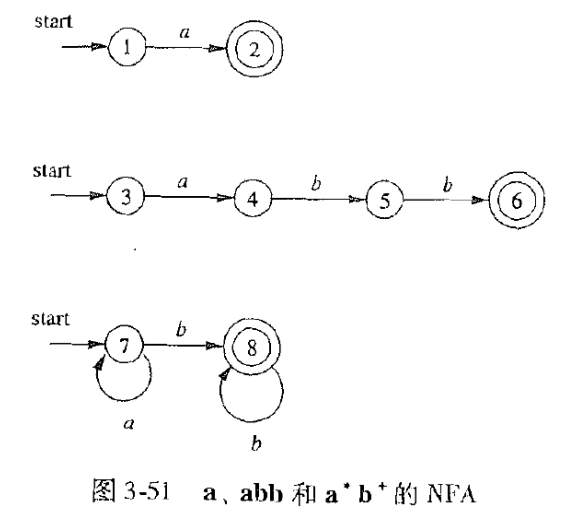
image-20221124164702365

合并这三个 NFA, 构造 $a|abb|a^*b^+$ 对应的 NFA

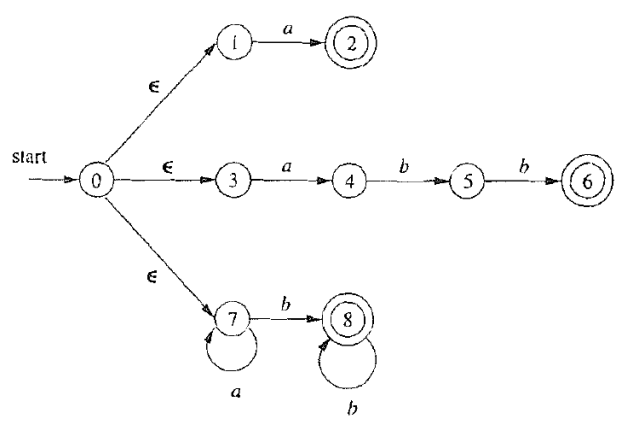
image-20221124164820073

6.2 使用子集构造法将 NFA 转化为等价的 DFA

  • 并消除 “死状态”

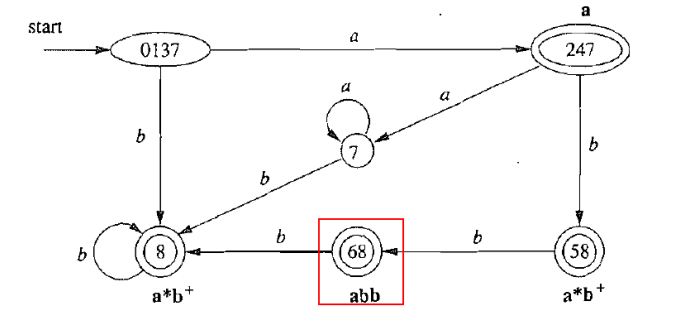
image-20221124164922855

  • 注意：要保留各个 NFA 的接受状态信息, 并采用最前优先匹配原则

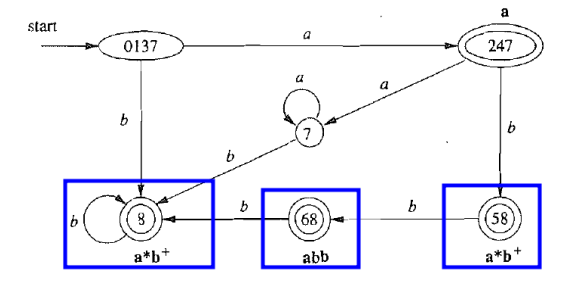
image-20221124170335679

  • $\forall a \in \Sigma.\delta(\emptyset, a) = \emptyset$
    • 需要消除 “死状态”, 避免词法分析器徒劳消耗输入流

模拟运行该 DFA, 直到无法继续为止 (输入结束或状态无转移);

  • 假设此时状态为 $s$

    • 若 $s$ 为接受状态, 则识别成功;

    • 否则, 回溯 (包括状态与输入流) 至最近一次经过的接受状态, 识别成功;

    • 若没有经过任何接受状态, 则报错 (忽略第一个字符)

    • 无论成功还是失败, 都从初始状态开始继续识别下一个词法单元

$x = a$ 输入结束; 接受; 识别出 $a$

$x = abba$ 状态无转移; 回溯成功; 识别出 $abb$

$x = aaaa$ 输入结束; 回溯成功; 识别出 $a$

$x = cabb$ 状态无转移; 回溯失败; 报错 $c$

6.3 特定于词法分析器的 DFA 最小化方法

image-20221124164922855

  • 初始划分需要考虑不同的词法单元
    • 不能直接把所有终止状态分为一类

$\Pi_0 = \set{\set{0137,7}, \textcolor{red}{\set{247}, \set{8, 58}, \set{68}}, \textcolor{green}{\set{\emptyset}}}$

$\Pi_1 = \set{\textcolor{blue}{\set{0137}, \set{7}}, \set{247}, \textcolor{blue}{\set{8}, \set{58}}, \set{68}}$

7. DFA $\Rightarrow$ RE

  • $D \Longrightarrow r$
  • 要求: $\textcolor{red}{L(r) = L(D)}$

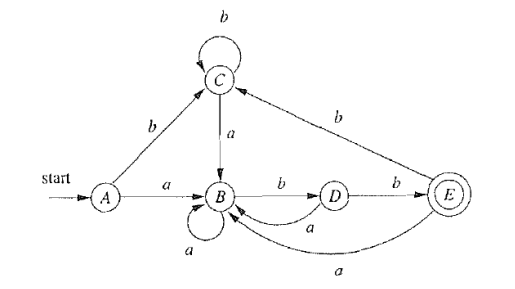
考虑下图 DFA

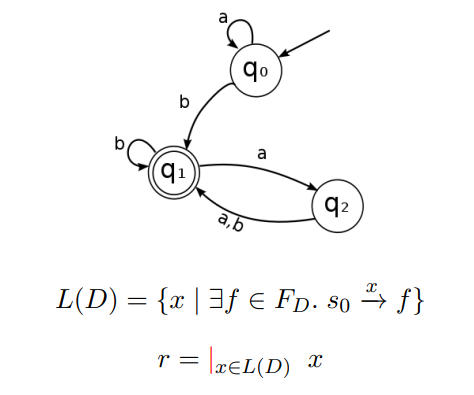
image-20221128162254029

  • 字符串 $x$ 对应于有向图中的路径
  • 求有向图中所有 (从初始状态到接受状态的) 路径
  • $\textcolor{red}{但是, 如果有向图中含有\textbf{环}, 则存在无穷多条路径}$
    • 不要怕, 我们有 Kleene 闭包(*)

Floyd-Warshall(弗洛伊德算法)

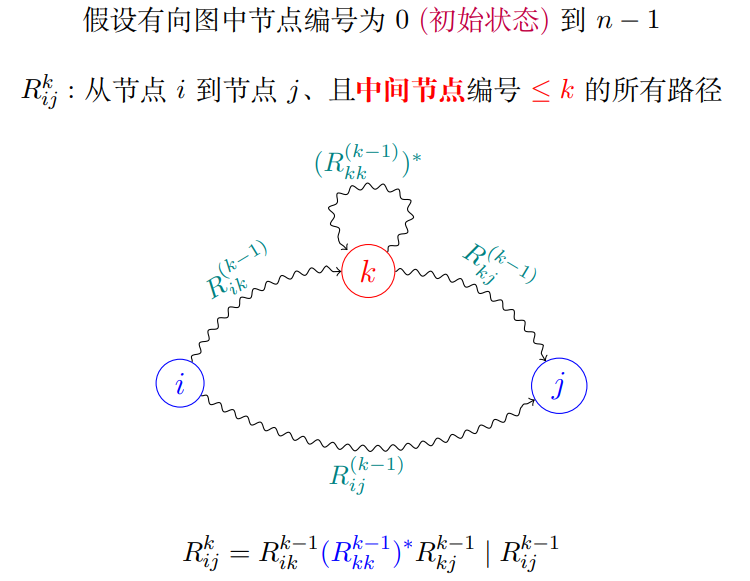
image-20221128163359324

如何初始化

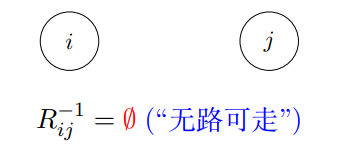
  • $R^{-1}_{ij}:$ 从节点 $i$ 到节点 $j$ 、且不经过中间节点的所有路径

  • 可以分为四种情况

    1. image-20221128163754963
    2. image-20221128163803715
    3. image-20221128163815739
    4. image-20221128163832278

  • 关于 $\textcolor{red}{\emptyset}$ (注意: 它不是正则表达式) 的规定

    • $\emptyset r = r\emptyset = \emptyset$
    • $\emptyset\mid r = r$

$r$ 的最终结果是什么

  • 求有向图中所有 (从初始状态到接受状态的) 路径

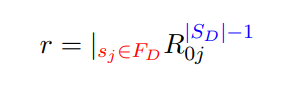
image-20221128164117771

image-20221128164145771

  • 应用到初始的 DFA

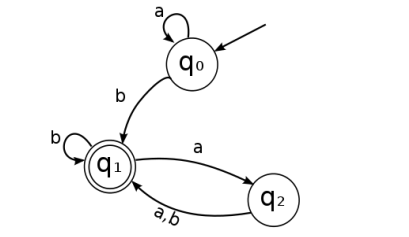
    image-20221128164252370

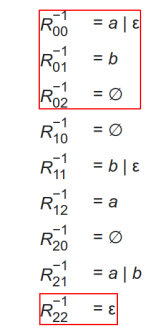
    image-20221128164304111

    1. image-20221128164344214
    2. image-20221128164357884
    3. image-20221128164415452

补充内容

龙书

2.6 词法分析

构成一个词法单元的输入字符序列称为词素(lexem)，词法分析器使得语法分析器不需要考虑词法单元的词素表示方式。

词法分析器使用一个表来保存字符串，从而解决了如下两个问题：

  • 单一表示。一个字符串表可以将编译器的其余部分和表中字符串的具体表示隔离开，因为编译器后面的步骤可以只使用指向表中字符串的指针或引用。操作引用要比操作字符串本身更加高效。
  • 保留字。要实现保留字，可以在初始化时在字符串表中加入保留的字符串以及它们对应的词法单元。当词法分析器读到一个可以组成标识符的字符串或词素时，它首先检查这个字符串表中是否有这个词素。如是，它就返回表中的词法单元，否则返回带有终结符号 id 的词法单元。

3.1 词法分析器的作用

词法分析器的主要任务是读入源程序的输入字符、将它们组成词素，生成并输出一个词法单元序列，每个词法单元对应于一个词素。

在某些情况下，词法分析器会从符号表中读取有关标识符种类的信息，以确定向语法分析器传送哪个词法单元。

词法分析器在编译器中负责读取源程序，因此它还会完成一些识别词素之外的其他任务。

  • 任务之一是过滤掉源程序中的注释和空白（空格、换行符、制表符以及在输入中用于分隔词法单元的其他字符）；
  • 另一个任务是将编译器生成的错误消息与源程序的位置联系起来。

有时，词法分析器可以分成两个级联的处理阶段

  • 扫描阶段主要负责完成一些不需要生成词法单元的简单处理，比如删除注释和将多个连续的空白字符压缩成一个字符。
  • 词法分析阶段是较为复杂的部分,它处理扫描阶段的输出并生成词法单元。
3.1.1 词法分析及语法分析

把编译过程的分析部分划分为词法分析和语法分析阶段有如下几个原因：

  • 最重要的考虑是简化编译器的设计
    • 将词法分析和语法分析分离通常使我们至少可以简化其中的一项任务

  • 提高编译器的效率

    • 把词法分析器独立出来使我们能够使用专用于词法分析任务、不进行语法分析的技术
    • 可以使用专门的用于读取输入字符的缓冲技术来显著提高编译器的速度

  • 增强编译器的可移植性

    • 输入设备相关的特殊性可以被限制在词法分析器中
3.1.2 词法单元、模式和词素

词法单元由一个词法单元名和一个可选的属性值组成。

  • 词法单元名是一个表示某种词法单位的抽象符号，比如一个特定的关键字，或者代表一个标识符的输入字符序列。
  • 词法单元名字是由语法分析器处理的输入符号。我们将使用词法单元的名字来引用一个词法单元。

模式描述了一个词法单元的词素可能具有的形式。

  • 当词法单元是一个关键字时，它的模式就是组成这个关键字的字符序列。
  • 对于标识符和其他词法单元，模式是一个更加复杂的结构，它可以和很多符号串匹配

词素是源程序中的一个字符序列

  • 它和某个词法单元的模式匹配，并被词法分析器识别为该词法单元的一个实例。

在C语句 printf("Total= % d\n",score); 中

printf和score都是和词法单元id的模式匹配的词素，而“Total =% d\n”则是一个和 literal 匹配的词素。

image-20221111153545862

在很多程序设计语言中，下面的类别覆盖了大部分或所有的词法单元:

  • 每个关键字有一个词法单元。一个关键字的模式就是该关键字本身
  • 表示运算符的词法单元。它可以表示单个运算符，也可以像上图中的comparison表示一类运算符
  • 一个表示所有标识符的词法单元
  • 一个或多个表示常量的词法单元，比如数字和字面值字符串
  • 每一个标点符号有一个词法单元，比如左右括号、逗号和分号
3.1.3 词法单元的属性

如果有多个词素可以和一个模式匹配，那么词法分析器必须向编译器的后续阶段提供有关被匹配词素的附加信息。

例如，0和1都能和词法单元number的模式匹配，但是对于代码生成器而言，至关重要的是知道在源程序中找到了哪个词素。

因此，在很多情况下，词法分析器不仅仅向语法分析器返回一个词法单元名字，还会返回一个描述该词法单元的词素的属性值

词法单元的名字将影响语法分析过程中的决定，而这个属性则会影响语法分析之后对这个词法单元的翻译。

我们假设一个词法单元至多有一个相关的属性值，这个属性值可能是一个组合了多种信息的结构化数据。

最重要的例子是词法单元id,我们通常会将很多信息和它关联。一般来说，和一个标识符有关的信息：例如它的词素、类型、它第一次出现的位置（在发出一个有关该标识符的错误消息时需要使用这个信息）都保存在符号表中。因此，一个标识符的属性值是一个指向符号表中该标识符对应条目的指针。

例如Fortran语句 E = M * C ** 2 中的词法单元名字和相关的属性值可写成如下的名字-属性对序列：

image-20221112141117200

在某些对中，特别是运算符、标点符号和关键字的对中，不需要有属性值

该例中，词法单元number有一个整数属性值。在实践中，编译器将保存一个代表该常量的字符串，并将一个指向该字符串的指针作为number的属性值。

3.1.4 词法错误

假设出现所有词法单元的模式都无法和剩余输入的某个前缀相匹配的情况，此时词法分析器就不能继续处理输入。当出现这种情况时，最简单的错误恢复策略是“恐慌模式”恢复。 我们从剩余的输入中不断删除字符，直到词法分析器能够在剩余输入的开头发现一个正确的词法单元为止。

这个恢复技术可能会给语法分析器带来混乱。但是在交互计算环境中，这个技术已经足够了。

可能采取的其他错误恢复动作包括：

  • 从剩余的输入中删除一个字符。
  • 向剩余的输入中插入一个遗漏的字符。
  • 用一个字符来替换另一个字符。
  • 交换两个相邻的字符

这些变换可以在试图修复错误输入时进行。最简单的策略是看一下是否可以通过一次变换将剩余输入的某个前缀变成一个合法的词素。

这种策略还是有道理的，因为在实践中，大多数词法错误只涉及一个字符。另外一种更加通用的改正策略是计算出最少需要多少次变换才能够把一个源程序转换成为一个只包含合法词素的程序。但是在实践中发现这种方法的代价太高，不值得使用。

3.2 输入缓冲

我们常常需要查看一个词素之后的若干字符才能够确定是否找到了正确的词素，比如，我们只有读取到一个非字母或数字的字符之后才能确定我们已经到达一个标识符的末尾

在C语言中，像 - 、= 或 ＜ 这样的单字符运算符也有可 能是->、==或 <= 这样的双字符运算符的开始字符

3.2.1 缓冲区对

通过两个交替读入的缓冲区来减少用于处理单个输入字符的时间开销。

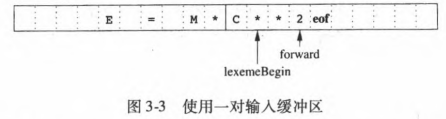
image-20221112143331856

每个缓冲区的容量都是 N 个字符，通常 N 是一个磁盘块的大小，如4096字节。我们可以使用系统读取命令一次将 N 个字符读入到缓冲区中，而不是每读入一个字符调用一次系统读取命令。如果输入文件中的剩余字符不足N个，那么就会有一个特殊字符(EOF)来标记源文件的结束。

程序为输入维护了两个指针:

  • lexemeBegin指针：该指针指向当前词素的开始处。当前我们正试图确定这个词素的结尾。
  • forward指针：它一直向前扫描，直到发现某个模式被匹配为止。

一旦确定了下一个词素，forward指针将指向该词素结尾的字符。词法分析器将这个词素作为某个返回给语法分析器的词法单元的属性值记录下来。然后使lexemeBegin指针指向刚刚找到的词素之后的第一个字符。

将forward指针前移要求我们首先检査是否已经到达某个缓冲区的末尾。如果是，我们必须将 N 个新字符读到另一个缓冲区中，且将forward指针指向这个新载入字符的缓冲区的头部。只要我们从不需要越过实际的词素向前看很远，以至于这个词素的长度加上我们向前看的距离大于 N, 我们就决不会在识别这个词素之前覆盖掉这个尚在缓冲区中的词素。

3.2.2 哨兵标记

如果我们采用上一节中描述的方案，那么在每次向前移动forward指针时，我们都必须检査是否到达了缓冲区的末尾。若是，那么我们必须加载另一个缓冲区。

因此每读入一个字符, 我们需要做两次测试：

  • 一次是检査是否到达缓冲区的末尾
  • 另一次是确定读入的字符是什么(可能是一个多路分支选择语句)。

如果我们扩展每个缓冲区，使它们在末尾包含一个“哨兵” (sentinel)字符，我们就可以把对缓冲区末端的测试和对当前字符的测试合二为一。这个哨兵字符必须是一个不会在源程序中出现的特殊字符，一个自然的选择就是字符EOF

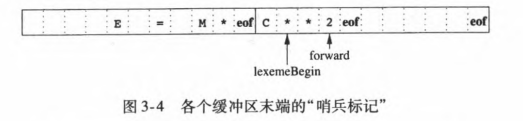
image-20221112144545736

  • 请注意，EOF仍然可以用来标记整个输入的结尾。任何不是出现在某个缓冲区末尾的EOF都表示到达了输入的结尾

image-20221112144649129

3.3 词法单元的规约

3.3.1 串和语言

串的各部分的术语

  1. 串 $s$ 的前缀(prefix)是从 $s$ 的尾部删除 0 个或多个符号后得到的串。例如,ban、banana 和 $\epsilon$ 是banana的前缀
  2. 串 $s$ 的后缀(suffix)是从 $s$ 的开始处删除 0 个或多个符号后得到的串。例如，nana、banana 和 $\epsilon$ 是banana的后缀。
  3. 串 $s$ 的子串(substring)是删除 $s$ 的某个前缀和某个后缀之后得到的串。例如，bnana、nan和 $\epsilon$ 是banana的子串。
  4. 串 $s$ 的真(true)前缀、真后缀、真子串分别是 $s$ 的既不等于 $\epsilon$ 也不等于 $s$ 本身的前缀、后缀和子串
  5. 串 $s$ 的子序列(subsequence)是从 $s$ 中删除 0 个或多个符号后得到的串，这些被删除的符号可能不相邻。例如，baan是banana的一个子序列
3.3.3 正则表达式

可以用一个正则表达式定义的语言叫做正则集合(regular set)。如果两个正则表达式 $r$ 和 $s$ 表示相同的语言，则称 $r$ 和 $s$ 等价(equivalent)，记作 $r$ = $s$ .

  • 例如 (a|b) = (b|a)

正则表达式遵守一些代数定律，每个定律都断言两个具有不同形式的表达式等价

image-20221115164950975

自制编译器

抽象语法树和节点

语法树和语法是完全对应的，所以例如 C 语言的终结符分号以及表达式两端的括号等都包含在真实的语法树中。

但是，保存分号和括号基本没有实际的意义，因此实际上大部分情况下会生成一开始就省略分号、括号等的抽象语法树。也就是说，解析器会跳过语法树，直接生成抽象语法树。

无论语法树还是抽象语法树，都是树形的数据结构，因此和普通的树结构相同，由称为节点（node）的数据结构组合而成。用 Java 来写的话，一个节点可以用一个节点对象来表示。

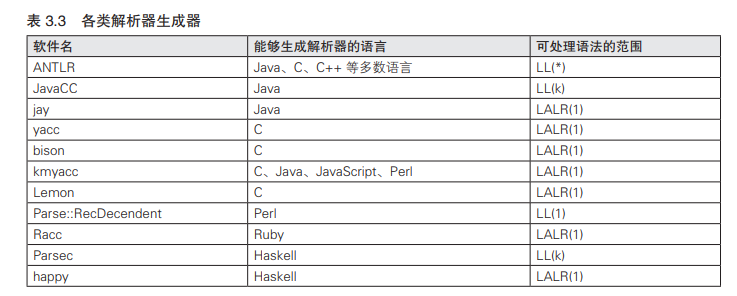
解析器生成器

生成扫描器的程序称为扫描器生成器（scanner generator），生成解析器的程序称为解析器生成器（parser generator）。只需指定需要解析的语法，扫描器生成器和解析器生成器就能生成解析相应语法的代码。

扫描器生成器都大体类似，解析器生成器则有若干个种类。现在具有代表性的解析器生成器可分为 LL 解析器生成器和 LALR 解析器生成器两类。

image-20221112161342539

image-20221112161400838

Prev
2023-08-09 14:53:19 # NJU # 编译原理
Next