编译原理(3) 语法分析
2023-08-09 14:53:19 # NJU # 编译原理

语法分析

一、ANTLR 4 语法分析器

1. 二义性文法

  • 二义性是不能接受的，必须消除

1.1 IfStat

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 不考虑 antlr 的处理, 单看文法这是有二义性的
stat : 'if' expr 'then' stat
     | 'if' expr 'then' stat 'else' stat
     | expr
     ;
     
/* 
 if a then if b then c else d
 此处 else d 归属是模糊的
*/

// 解决方法非常复杂:
// 将 else 与最近的未被匹配的 if 匹配
stat : matched_stat | open_stat ;

matched_stat : 'if' expr 'then' matched_stat 'else' matched_stat
             | expr
             ;

open_stat: 'if' expr 'then' stat
         | 'if' expr 'then' matched_stat 'else' open_stat
         ;

Q: 如何判断文法有没有二义性

A: 做不到, 只能靠经验

Q: ANTLR 如何解决二义性问题

A: 通过书写规则的顺序来决定优先级, 优先解释为优先级高的结构

1.2 Left-Factoring

1
2
3
4
5
6
7
8
9
stat : 'if' expr 'then' stat
     | 'if' expr 'then' stat 'else' stat
     | expr
     ;
==============================================
stat : 'if' expr 'then' stat stat_prime ;
stat_prime : 'else' stat
     |
     ;
  • 很明显, 提取左公因子无助于消除文法二义性
  • ANTLR 4 可以处理有左公因子的文法

1.3 Expr

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
expr :
  | expr '*' expr
  | expr '-' expr
  | DIGIT
  ;

// 同样存在二义性
1-2-3 -> (1-2)-3 | 1-(2-3)
1-2*3 -> (1-2)*3 | 1-(2*3)

// 解决方法, 但是引入很多冗余文法符号
// 左递归文法, expr 只有左侧的 expr 是递归的
expr : expr '-' term
     | term
     ;
     
term : term '*' factor
     | factor
     ;
     
factor : DIGIT ;

// 右递归文法, 也能解决优先级, 但会改变结合性 1-2-3 -> 1-(2-3)
expr : term expr_prime ;
expr_prime : '-' term expr_prime
     |
     ;
     
term : factor term_prime ;
term_prime : '*' factor term_prime
     |
     ;
     
factor : DIGIT ;
  • 左递归(左结合)，右递归(右结合)
  • ANTLR 4 可以处理(直接)左递归
    • 写在上方的规则优先级高
    • 但是有些情况需要右结合(^)
      • 二元运算符需要特别标记 <assoc = right> expr '^' expr
      • 一元运算符不需要标记，因为只能解释为右结合 ------1

2. Call Graphs

2.1 监听器模式(Listener)

  • ANTLR 通过深度优先遍历生成的语法树

    • 除了叶子节点, 所有的内部节点至少会经过两次
    • ANTLR 会为其生成 ENTERXXX(), EXITXXX() 的方法

  • 一条规则有不同选择时, 通过添加 #label 来区分, 单个选择内部使用 op 来区分

    • ANTLR 会生成对应的 ENTER\EXIT LABEL 方法, op 则作为成员变量
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    expr: ID '(' exprList? ')'    # Call // function call
        | expr '[' expr ']'       # Index // array subscripts
        | op = '-' expr                # Negate // right association
        | op = '!' expr                # Not // right association
        | <assoc = right> expr '^' expr # Power
        | lhs = expr (op = '*'| op = '/') rhs = expr     # MultDiv
        | lhs = expr (op = '+'| op = '-') rhs = expr     # AddSub
        | lhs = expr (op = '==' | op = '!=') rhs = expr  # EQNE
        | '(' expr ')'            # Parens
        | ID                      # Id
        | INT                     # Int
        ;

    image-20221122164530981

2.2 访问者模式(Visitor)

  • 详见实验

  • Visitor在访问每个节点的子节点前会调用visitChildren()函数

  • Visitor在访问每个终结符节点时会调用visitTerminal()函数
  • 对于每一个语法规则都存在一个对应的visit函数，如 exp 规则对应的函数为visitExp()

3. 上下文无关文法

3.1 语法

Definition (Context-Free Grammar (CFG); 上下文无关文法)

上下文无关文法 $G$ 是一个四元组 $G = (T,N,P,S):$

  • $T$ 是终结符号 (Terminal) 集合, 对应于词法分析器产生的词法单元;

  • $N$ 是非终结符号 (Non-terminal) 集合;

  • $P$ 是产生式 (Production) 集合;

    • $A \in N \longrightarrow α \in (T \cup N)^\ast$

    • 头部/左部 (Head) $A$: 单个非终结符

    • 体部/右部 (Body) $α$: 终结符与非终结符构成的串, 也可以是空串 $\epsilon$

  • $S$ 为开始 (Start) 符号。要求 $S \in N$ 且唯一。

image-20221124173937897

3.2 语义

上下文无关文法 $G$ 定义了一个语言 $L(G)$

  • 语言是串的集合
  • 串从何来?
推导 (Derivation)
  • 推导即是将某个产生式的左边替换成它的右边
  • 每一步推导需要选择替换哪个非终结符号, 以及使用哪个产生式

$E \to E + E \mid E \ast E \mid (E) \mid -E \mid \bf id$

  • $E \implies -E \implies -(E) \implies -(E + E) \implies -(\textbf{id} + E) \implies -(\textbf{id} + \textbf{id})$
  • $E \implies -E \implies -(E) \implies -(E + E) \implies \textcolor{blue}{-(E + \textbf{id})} \implies -(\textbf{id} + \textbf{id})$

$E \implies -E:$ 经过一步推导得出

$E \stackrel{+}{\implies} -(\textbf{id} + E):$ 经过一步或多步推导得出

$E \stackrel{\ast}{\implies} -(\textbf{id} + E):$ 经过零步或多步推导得出

Definition (Sentential Form; 句型)

如果 $S \stackrel{\ast}{\implies} \alpha ,$ 且 $ \alpha \in (T \cup N)^\ast ,$ 则称 $\alpha$ 是文法 $G$ 的一个句型

  • $E \to E + E \mid E \ast E \mid (E) \mid -E \mid \bf id$
  • $E \implies -E \implies -(E) \implies -(E + E) \implies -(\textbf{id} + E) \implies -(\textbf{id} + \textbf{id})$
    • 夹杂着终结符和非终结符的串都叫做句型
Definition (Sentence; 句子)

如果 $S \stackrel{\ast}{\implies} w ,$ 且 $w \in T^\ast ,$ 则称 $w$ 是文法 $G$ 的一个句子

Definition (文法 $G$ 生成的语言 $L(G)$)

文法 $G$ 的语言 $L(G)$ 是它能推导出的所有句子构成的集合。

  • $w \in L(G) \iff S \stackrel{\ast}{\Rightarrow} w$

3.3 关于文法 $G$ 的两个基本问题

  • Membership问题: 给定字符串 $x \in \textcolor{red}{T^\ast} , x \in L(G)$ ?

  • $L(G)$ 究竟是什么?

3.3.1 给定字符串 $x \in T^\ast , x \in L(G)$ ?

  • 即, 检查 $x$ 是否符合文法 $G$

  • 这就是语法分析器的任务:

    • 为输入的词法单元流寻找推导、构建语法分析树, 或者报错
3.3.2 $L(G)$ 是什么?

  • 这是程序设计语言设计者需要考虑的问题

  • 一些例子

    • $L(G) = \set{良匹配括号串}$

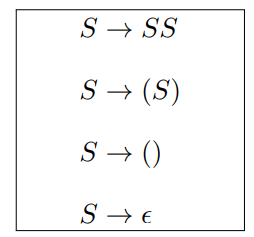
      image-20221126144503343

    • $L(G) = \set{a^nb^n \mid n \ge 0}$

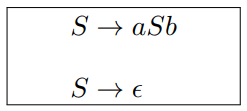
      image-20221126144707716

    • $字母表 \Sigma = \set{a, b} 上的所有 \textcolor{blue}{\textbf{回文串}} (Palindrome) 构成的语言$

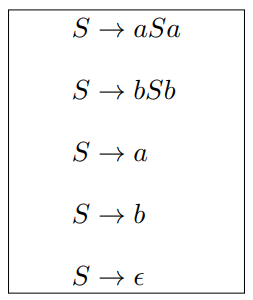
      image-20221126144933786

    • $\set{b^na^mb^{2n} \mid n \ge 0, m \ge 0}$

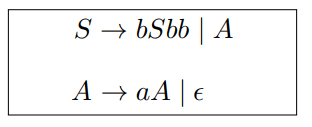
      image-20221126145059081

    • $\set{x \in \set{a, b}^\ast \mid x 中 a, b 个数 \textcolor{red}{\textbf{相同}}}$

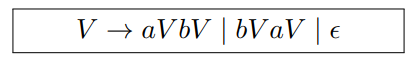
      image-20221126145228086

      • $a, b$ 开头是对称的, 此处只考虑 $a$ 开头
      • 一定存在一个 $b$ 使得按这个 $b$ 分割的两个串中 $a, b$ 个数相同

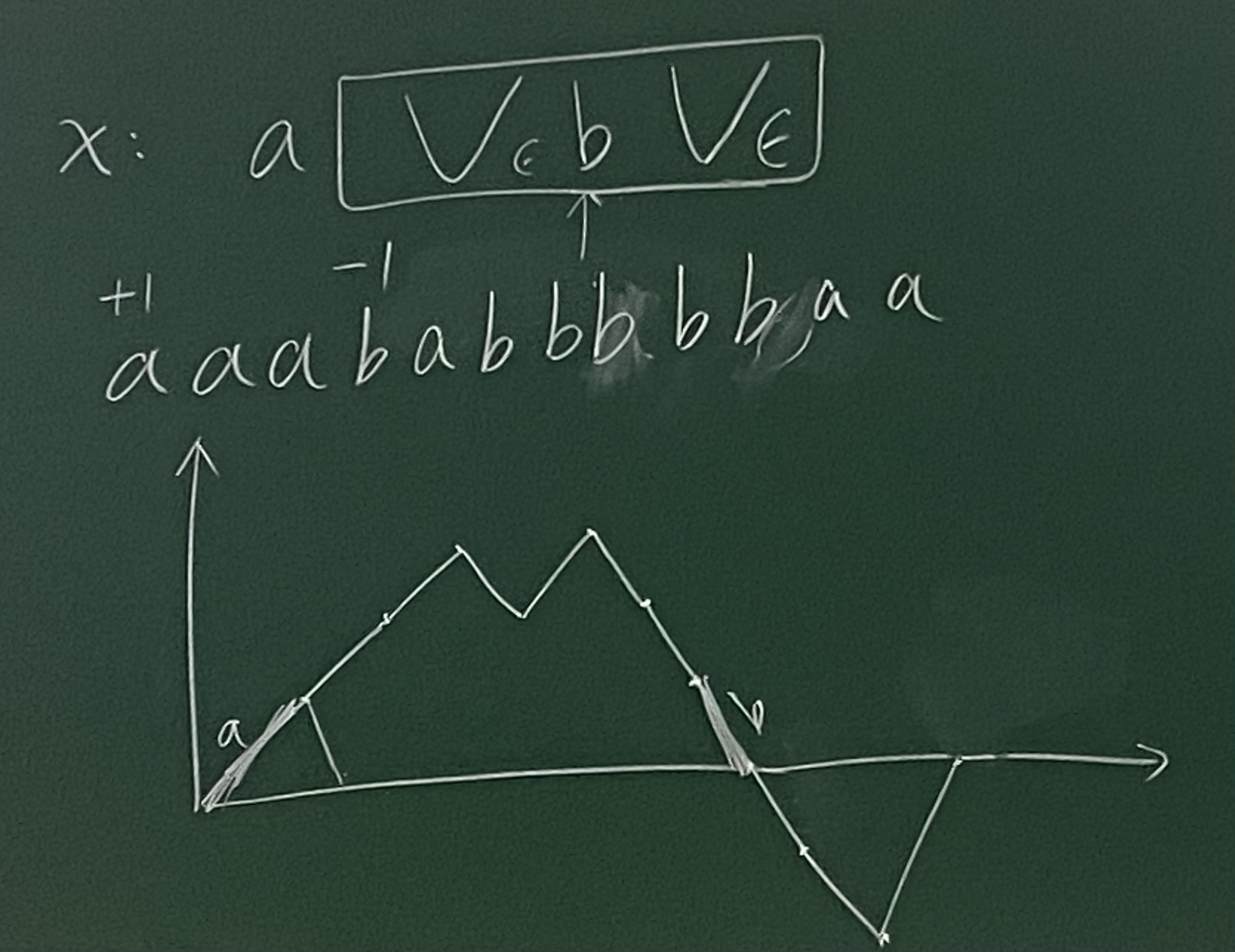
      image-20221126145544058

  • $\set{x \in \set{a, b}^\ast \mid x 中 a, b 个数 \textcolor{red}{\textbf{不同}}}$

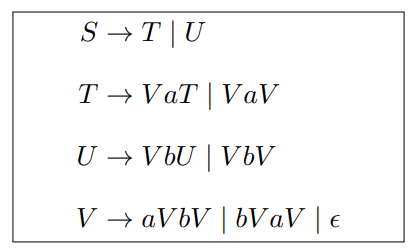
    image-20221126150206032

4 正则表达式

为什么不使用优雅、强大的正则表达式描述程序设计语言的语法?

  • 正则表达式的表达能力严格弱于上下文无关文法

image-20221126150328339

4.1 RE $\rightarrow$ CFG

每个正则表达式 $r$ 对应的语言 $L(r)$ 都可以使用上下文无关文法来描述

  • RE

    • $r = (a \mid b)^\ast abb$

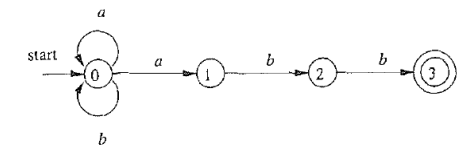
    image-20221126151201551

  • CFG

    image-20221126151258746

4.2 CFG $\rightarrow$ RE 反例

  • CFG

    • $L = \set{a^nb^n \mid n \ge 0}$

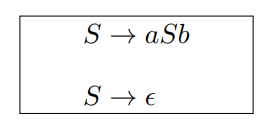
      image-20221126151604143

  • RE

    • 该语言无法使用正则表达式来描述

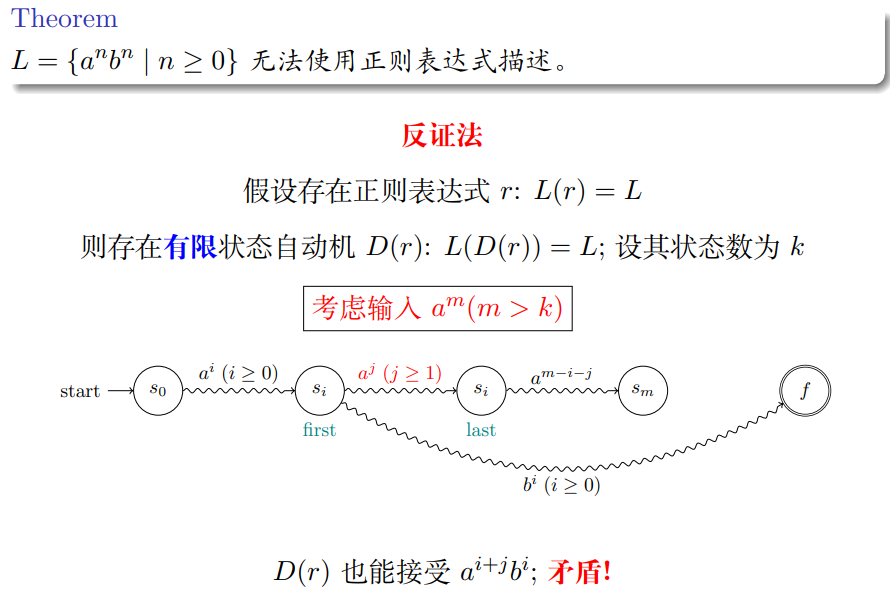
image-20221126151732638

  • 因为 $m \gt k$, 所以一定会有状态经过了不止一次, 假设就是 $s_i$, 上图画出第一次碰到和最后一次碰到的状态
    • 第一次到最后一次中间消耗的 $a$ 的个数一定 $\ge 1$
  • 假设消耗掉 $a^i$ 后第一次到达 $s_i$, 此时接收 $b^i$ 后根据假设应当到达终止状态 $f$
    • 但因为第一次到达和最后一次到达的 $s_i$ 是相同的状态, 因此也应当可以接受 $a^{i+j}b^i$
    • 矛盾！

  • 该反例称为泵引理, Pumping Lemma

    image-20221126153050203

二、递归下降的$LL(1)$语法分析器

1. 背景介绍

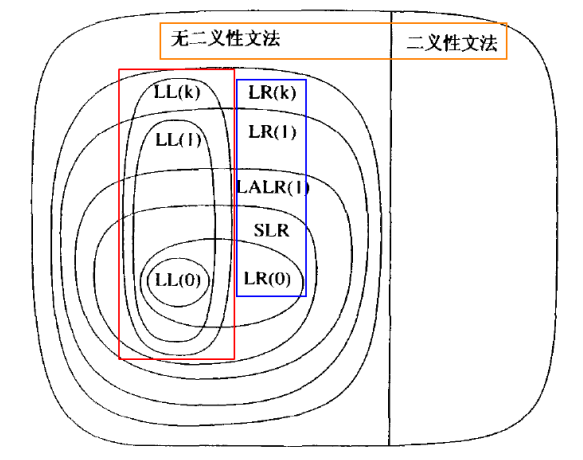
语法分析算法可分为两类: $LL$, $LR$

  • $LR$ 更加复杂

构建语法分析树: 自顶向下 $vs.$ 自底向上

  • $LL$ 为自顶向下
  • $LR$ 为自底向上

image-20221129212330806

只考虑无二义性的文法

  • 这意味着, 每个句子对应唯一的一棵语法分析树
  • 本节主题: $LL(1)$ 语法分析器

image-20221129212519129

ANTLR

image-20221129212642012

2. 什么是$LL(1)$语法分析器

  • 自顶向下的、
  • 递归下降的、
  • 基于预测分析表的、
  • 适用于$\textcolor{red}{LL(1) \textbf{文法}}$的、
  • $LL(1)$ 语法分析器

image-20221130144459907

2.1 自顶向下

$\textcolor{red}{\textbf{自顶向下}}构建语法分析树$

  • $\textcolor{blue}{\textbf{根节点}}是文法的起始符号$ $S$
  • $每个\textcolor{blue}{\textbf{中间节点}}表示\textcolor{purple}{\textbf{对某个非终结符应用某个产生式进行推导}}$
    • $\textcolor{red}{Q:}选择哪个非终结符, 以及选择哪个产生式$
  • $\textcolor{blue}{\textbf{叶节点}}是词法单元流$ $w\$$
    • $仅包含终结符号与特殊的\textcolor{teal}{\textbf{文件结束符}}$ $\textcolor{teal}{\$}$ $\textcolor{teal}{\texttt{(EOF)}}$
如何选择非终结符
  • 在推导的每一步, $L\textcolor{red}{L}(1)$ 总是选择最左边的非终结符进行展开
    • Leftmost derivation, 最左推导
  • $\textcolor{red}{L}L(1)$: 从左向右读入词法单元

2.2 递归下降

$\textcolor{red}{\textbf{递归}}\textcolor{blue}{\textbf{下降}}的典型实现框架$

image-20221129215551497

  • 为每个非终结符写一个递归函数
  • 内部按需调用其它非终结符对应的递归函数, 下降一层
递归下降示例

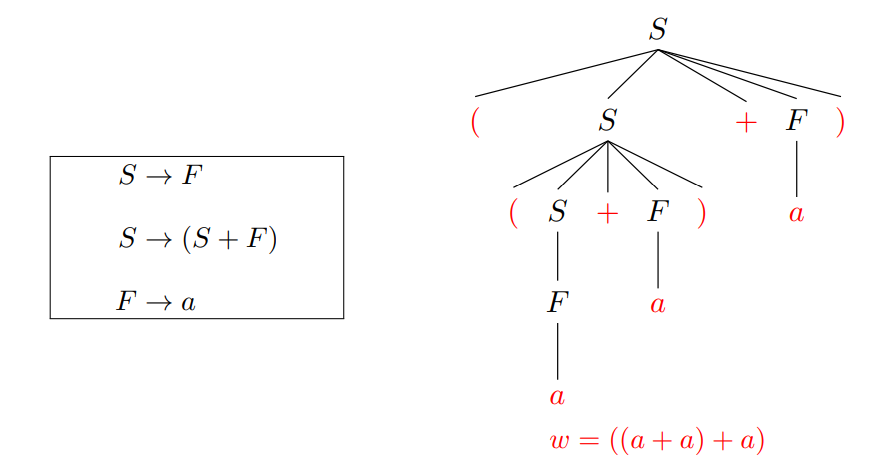
image-20221129222116911

  • 每次都选择语法分析树最左边的非终结符进行展开

$Q: 同样是展开非终结符 S, 为什么前两次选择了 S \to (S + F), 而第三次选择了 S \to F$ $?$

  • 因为它们面对的当前词法单元不同

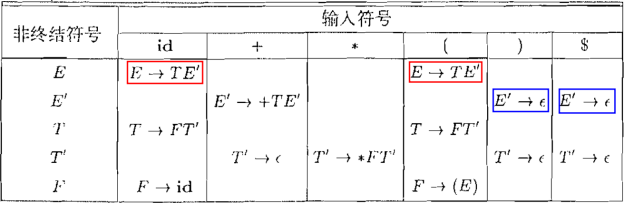
2.3 预测分析表

$使用\textcolor{red}{\textbf{预测分析表}}确定产生式$

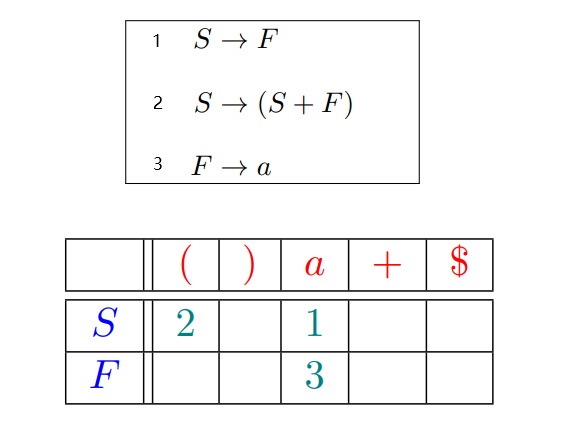
image-20221129222546435

  • $指明了每个\textcolor{blue}{\textbf{非终结符}}在面对不同的\textcolor{red}{\textbf{词法单元或文件结束符}}时,$

    $该选择哪个\textcolor{teal}{\textbf{产生式}} (按编号进行索引) 或者\textcolor{cyan}{\textbf{报错}} (空单元格)$

2.4 Definition ($LL(1)$ 文法)

$如果文法$ $G$ 的$\textcolor{red}{\textbf{预测分析表}}是\textcolor{blue}{\textbf{无冲突}}的, 则$ $G$ $是$ $LL(1)$ $文法$

  • $\textcolor{blue}{\textbf{无冲突}}: 每个单元格里只有一个产生式 (编号)$

  • $对于当前选择的\textcolor{blue}{\textbf{非终结符}},$

    $仅根据输入中\textcolor{red}{\textbf{当前的词法单元}} (LL(\textcolor{red}{1}))$ $即可确定需要使用哪条\textcolor{teal}{\textbf{产生式}}$

递归下降的、预测分析实现方法

image-20221129222546435

image-20221129224308689

image-20221129224316884

image-20221129224326342

3. 计算给定文法 $G$ 的预测分析表

3.1 引入

image-20221129225435287

  • 重点在于 optional_init 展开时如何选择
  • 非终结符展开要考虑两件事
    • 最左侧的终结符是不是所需要的
    • 如果要展开的非终结符的一个备选分支是 $\epsilon$, 后面的字符是不是所需要的

3.2 FIRST($\alpha$)

image-20221129231109091

image-20221129231302198

3.3 FOLLOW($A$)

image-20221129231515371

image-20221129231529491

3.4 计算FIRST,FOLLOW

3.4.1 FIRST
  1. image-20221129232019642
    • 只有前面所有非终结符都能推出 $\epsilon$, 才需要考虑下一个
  2. image-20221129232037559

举例

image-20221130141836513

3.4.2 FOLLOW

image-20221130142137823

举例

image-20221130142657320

image-20221130142720412

3.5 计算预测分析表

image-20221204172348302

image-20221204172356127

当下的选择未必正确, 但 “你别无选择”

image-20221130144017088

什么是 $LL(0)$ : 每个非终结符只有一条产生式

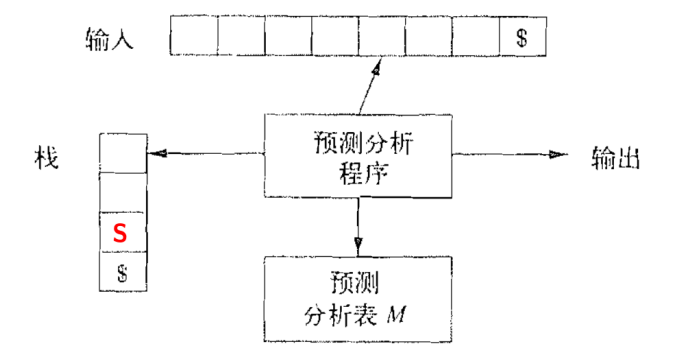
4. 非递归的预测分析算法

S: 初始符号

image-20221130144758691

image-20221130144842886

5. 非$LL(1)$文法如何解决

改造他!

  • 消除左递归
  • 提取左公因子

5.1 提取左公因子

1
2
3
4
5
x -> aB | aC	// 这种情况开始都有 a, 不知道要使用哪条

// 改造为
x -> aD
D -> B | C
  • antlr 不需要这么处理, 会使用更好的技术来处理

5.2 消除左递归

image-20221204173936840

  • 但是左递归文法在使用$LL(1)$文法的情况下是不能运行的
  • $LL(1)$文法需要为 $E$ 写一个递归函数
  • $E 在 \textcolor{red}{\textbf{不消耗任何词法单元}}的情况下, 直接递归调用 E, 造成\textcolor{green}{\textbf{死循环}}$

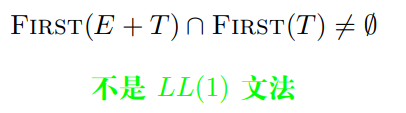
image-20221204174331739

右递归

如果一定要使用$LL(1)$文法，可以改为右递归

image-20221204174513260

image-20221204174554340

5.3 文件结束符 \$ 的必要性

image-20221204174726446

  • 观察蓝框, 在输入结束的情况下, 栈中还有内容, 此时就需要利用 \$ 来清空

三、Adaptive $LL(\ast)$ 语法分析算法

1. ANTLR 4

image-20221204223047803

直接左递归: E -> E + T

间接左递归: A -> B, B -> A

image-20221204224354903

courses-at-nju-by-hfwei/compilers-papers-we-love

2. 直接左递归与优先级

2.1 引入

image-20221204224547753

1
2
3
4
5
6
7
8
9
// parser-allstar/LRExpr.g4

stat : expr ';' EOF;

expr : expr '*' expr
     | expr '+' expr
     | INT
     | ID
     ;

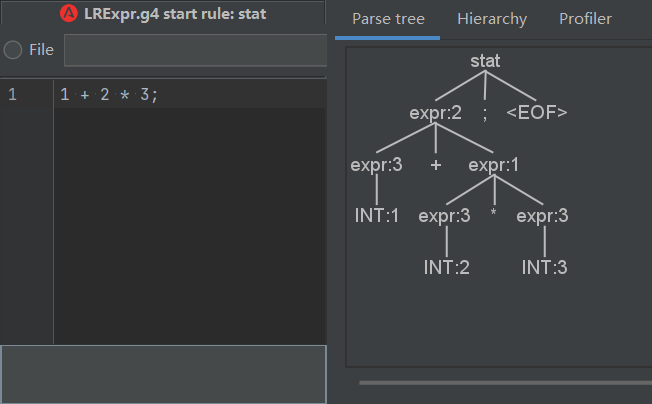
image-20221205143936396

优先级体现在 * 比 + 深一层

换言之，以上图为例，要考虑 expr:1 在哪一层展开

  • 和 + 同一层, 即上图情况, 则 * 更深, 优先级更高
  • 和的父节点一层, 则 + 与 * 优先级相同

image-20221205144439777

2.2 ANTLR 处理方法(优先级上升算法)

antlr4 LRExpr -Xlog

  • 添加 -Xlog 可以查看被 antlr4 重写后的文法

image-20221205144716053

$\Longrightarrow$

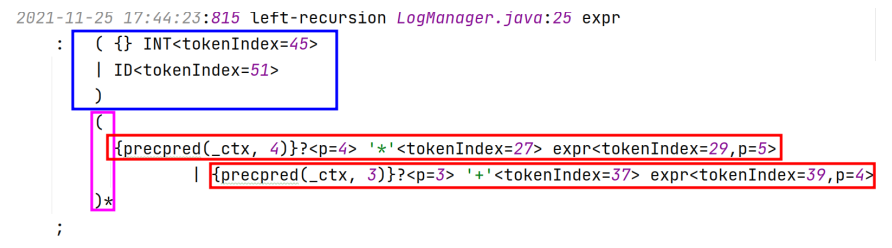
image-20221205144800009

$\stackrel{简化一下}{\Longrightarrow}$

image-20221205144906176

可以先简单看作 $(\texttt{INT} \mid \texttt{ID})(\ast E \mid + E)^\ast$

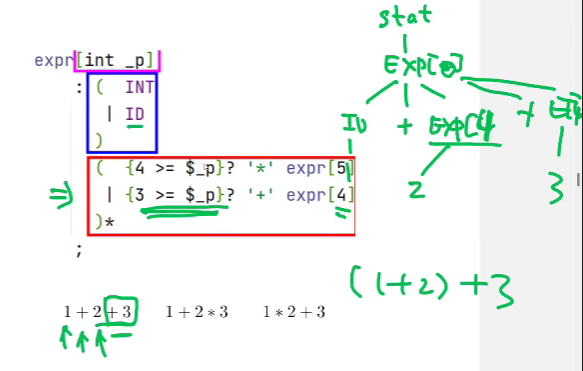
重点: 提供了一个优先级参数 _p

  • antlr4中, 优先级从上至下以此降低, 最底层优先级为 1, 每往上一层 +1
    • ID-1, INT-2, (expr ‘+’ expr)-3, (expr ‘*‘ expr)-4

举例

1 + 2 + 3

image-20221205151912558

  • 当遇到最后的 +3 时, 因为优先级限制不能直接展开, 否则就变成右结合了

  • exp[4] 中的 4 限制了要在哪一层展开, 这一层不满足, 要返回到上一层

image-20221205152206296

  • 在上一层展开 就变为 ID '+' EXP[4] '+' EXP[4]

1 + 2 * 3

image-20221205152508686

1 * 2 + 3

image-20221205152655882

2.3 扩展一下语法

  1. image-20221205152929622

    • 非常简单，因为不是左递归，处理时和 INT ID 一组

  2. image-20221205153045251

    • '-' expr 非左递归, 尽管优先级高, 处理时和 ID 一组

    image-20221205153149299

举例

-a + b! $\implies$ (-a) + (b!)

image-20221205153459054

-a!!

image-20221205154249678

  1. image-20221205161948138
    • 为了实现幂运算的右结合, 推导幂运算是, expr的优先级仍然是 expr[3]

举例

1\^2\^3 + 4

2.4 如何决定优先级

image-20221205162834597

3. 错误报告与恢复

3.1 引入

image-20221205162938835

image-20221205163008937

短短 10 行的代码竟出现 100 个错误,

  • 说明不是遇到错误就停下来

3.2 恐慌/应急(Panic)模式

  • 假装成功、调整状态、继续进行

image-20221205163248878

单词法符号移除

image-20221205163551701

单词法符号补全

image-20221205163601281

  • 但这种方法只能解决简单的错误, 复杂可使用 “同步-返回” 策略

3.3 同步-返回 策略

image-20221205163621087

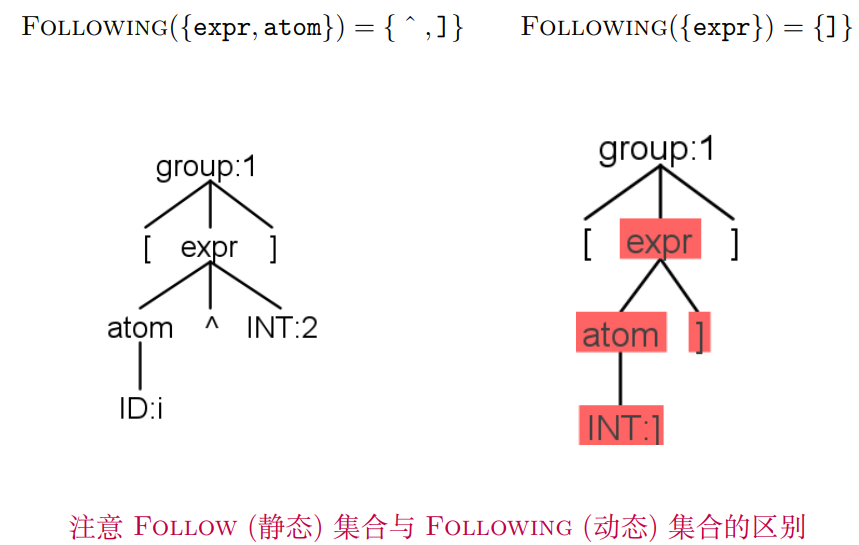
image-20221205164406514

静态与动态的区别

例如图右侧, 因为group匹配的是第一条规则, expr跟着的只可能是 ‘]’, 而不包括 ‘)’

image-20221205164851153

4. Adaptive $LL(\ast)$

image-20221205165442256

$A: a^\ast b$

  1. 为每个非终结符构造ATN网络

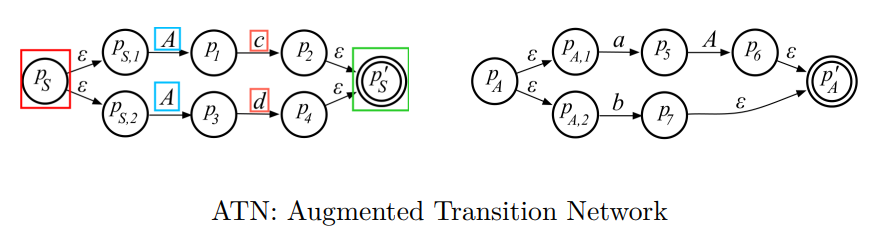
image-20221205165458601

  1. 根据ATN网络, 构造”向前看DFA”

image-20221205172932199

要点:

image-20221205171258755

示例:

image-20221205173007857

$D_0$: 初始状态

$f_{1/2}$: 第1/2条备选分支

第一个分量: 状态名

第二个分量: 当前子解析器在探索第几条分支

第三个分量: 递归调用的符号组成的栈

粗体是通过 move 得到，其他都是通过 闭包 得到的

Prev
2023-08-09 14:53:19 # NJU # 编译原理
Next