数据库开发(2) 索引结构及使用
1. 索引是一种快捷访问方式
二分搜索树(BST,Binary Search Trees)
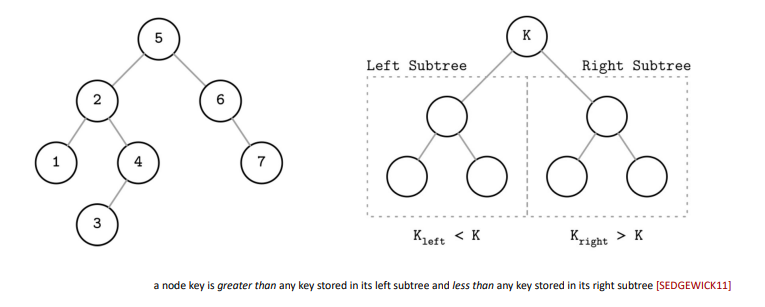
为什么要 Tree Balancing?
| $O(log_2N)$ | $O(N)$ |
|---|---|
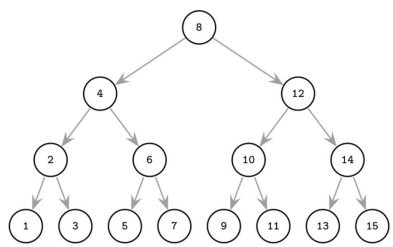 |
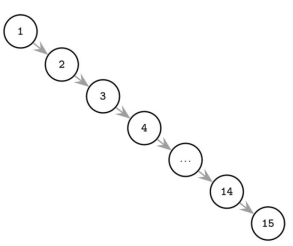 |
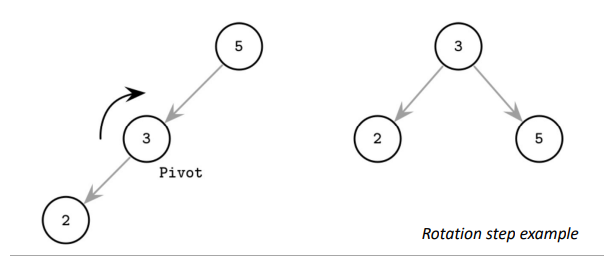
怎么做 Tree Balancing?
HDD和SSDs的差异
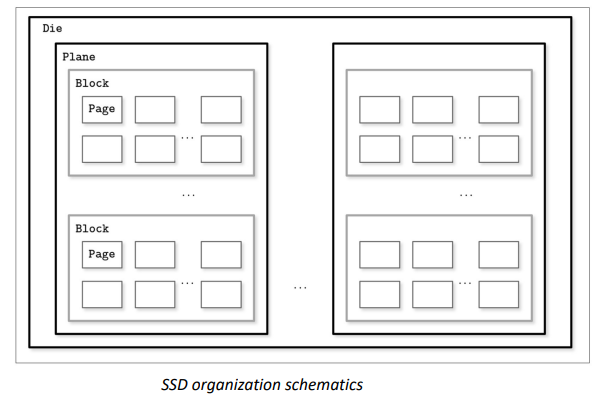
Block:最小的写单元,64-512 Page
Page:最小的读单元,2KB-16KB
SSD不过于像HDD⼀样非常强调随机 I/O和顺序I/O的差别,因为延迟差异不是很⼤。但是,预取、读取连续页和内部并⾏等⽅面,⼆者差距依旧存在[GOOSSAERT14]
逻辑图和实现结构图的差异
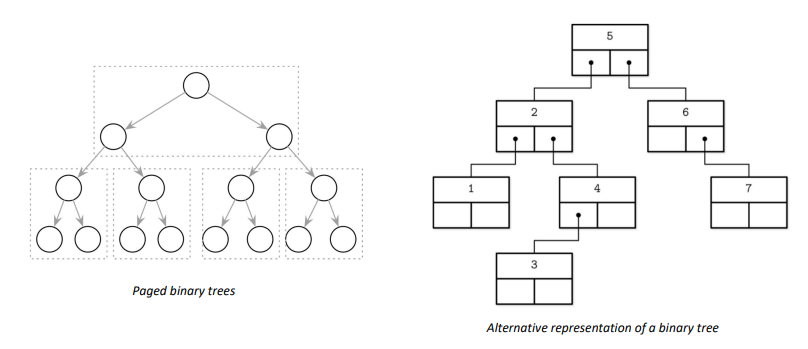
基于磁盘的索引结构
对于特定数据结构,有些更适用于磁盘,⽽有些更适用于内存
平台级软件,和硬件的关系非常⼤(操作系统、数据库、嵌⼊式、芯片……)
更适合磁盘实现的树必须具备以下属性
- ⾼扇出,以改善临近键的数据局限性
- 低⾼度,以减少遍历期间的寻道次数
2. B树索引的结构和应用
B-Tree(B+Tree)结构
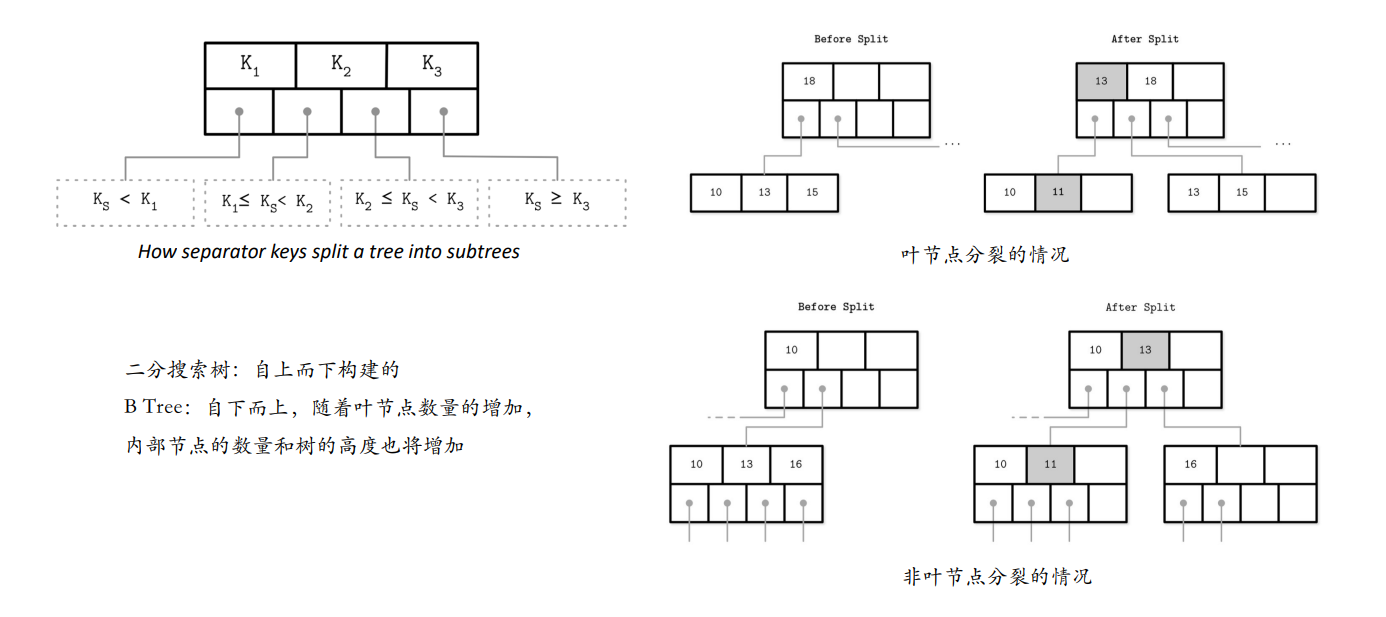
B树查找算法
查找,从根节点到叶节点的单向遍历
从根节点上执⾏⼆分搜索算法,将要搜索的$K$,与存储在根节点中的$K_n$进⾏比较,直到找到⼤于$K$的第⼀个分隔键,这样定位了⼀个要搜索的⼦树,顺着相应指针继续相同的搜索过程,直到目标叶节点,找到数据主⽂件指针
B-Tree(B+Tree)的逻辑存储结构

一次I/O:一次 Block 的读写,每个矩形就是一个 Block
对于硬件,只有 Block 锁,可以在内存添加 Page 锁
B+树深度固定在3-4
rowid:指向基本表的指针
B+树索引能做什么?
- 全键值:
where x = 123(depth + 1次的固定次数) - 键值范围:
where 45 < x < 123(先进行x=45,然后顺序读取直到x>=123) - 键前缀查找:
where x LIKE 'J%'
索引对数据的访问只是第一步
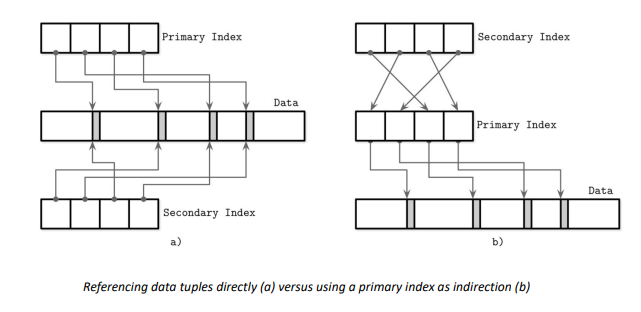
主键默认增加索引
两种方案:
- 方案一数据更新时会影响多个索引,但是快
- 方案二数据更新时只会影响一个索引