返回首页

情绪传播机制--相关文献调研

2025-07-05 暑假 科研
1111 字 6 分钟
情绪传播机制--相关文献调研
目录 ⌄
内容时效性提醒

"本篇博客完成日期距现在已大于一年，内容可能已过时，相关技术、政策或情况可能已发生变化，建议读者查证最新信息。"

An agent-based model for emotion contagion and competition in online social media#

文献

项目目的#

  • 综合 “情绪相关性”、“情绪传播与网络结构的耦合性”
  • 提出了一个结合“情绪影响力和联系强度偏好特征”的情绪传染模型

网络结构基本信息#

采用推特上真实数据集构建的有向网络结构:

  1. 节点:推特账户
  2. 边:账号关注的有向边
  3. 边权重:关系强度（共同好友、互相关注、互相转发量）
  4. 信息列表:（发送方 id + 带有情绪 i 的文章）

信息传播关键步骤#

  1. 推文发表
    固定概率 PP 决定是否发表，文章在发表时被赋予情绪，不随转发改变。

  2. 推文转发
    如果未发送推文，用户会在信息列表中查询，若转发倾向 tt 大于阈值 t0t_0，就会转发。

  3. 推文接收
    接收来自关注对象的推文，加入信息列表；若列表满，则删最早的。

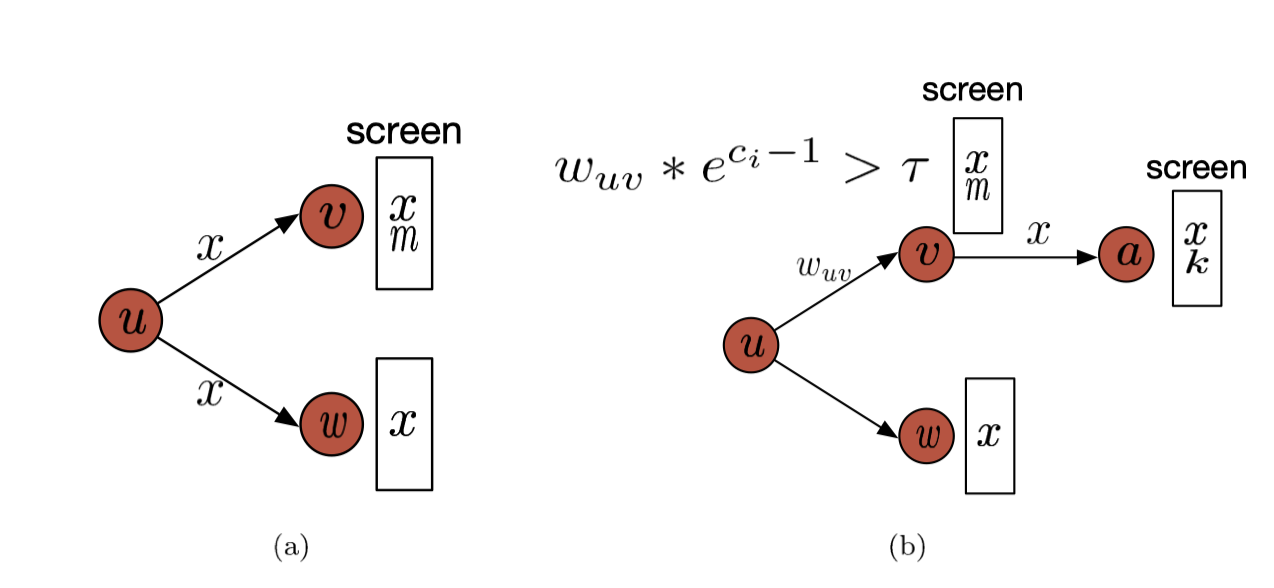
相关计算公式#

  1. 转发倾向:

    t=边权重×情绪相关性t = \text{边权重} \times \text{情绪相关性}

  2. 情绪:由固定概率赋予（根据推特数据集）

  3. 是否发表:固定概率决定

信息传播流程#

  1. 随机选择用户 UU
    2.1 以概率 PP 选择推文发送，发给所有关注者
    2.2 以概率 1−P1 - P 查看信息列表，若满足条件则转发推文给所有关注者

Agent-Based Simulations of Emotional Dialogs in the Online Social Network MySpace#

文献

研究内容和目的#

通过模拟社交网络，理解在线社交平台中的情绪传播机制。
情绪传播非随机，受网络结构、用户活跃度、情绪本身特性影响，具有迁移性，参数从数据集中推断。

网络结构基本信息#

数据来自 MySpace 用户之间公开可用的对话集:

  1. 节点:社交用户
  2. 边:消息发送形成的有向边
  3. 边权重:消息总数
  4. 情感变量:
    • 效价 vi(t)v_i(t) 表示情绪正负强度，范围 [−1,1][-1,1]
    • 唤醒度 ai(t)a_i(t) 表示活跃性，范围 [0,1][0,1]

更新方式如下:

  1. vi(t+1)=(1−γa)vi(t)+δθi,1Fv(t)v_{i}(t+1) = (1 - \gamma_a) v_{i}(t) + \delta_{\theta_i,1} \mathcal{F}_v(t)
  2. ai(t+1)=(1−γa)ai(t)+δθi,1Fa(t)a_{i}(t+1) = (1 - \gamma_a) a_{i}(t) + \delta_{\theta_i,1} \mathcal{F}_a(t)

相关概念:
γa\gamma_a 为常数，δθi,1\delta_{\theta_i,1} 为 Kronecker delta 函数，Fv(t),Fa(t)\mathcal{F}_v(t), \mathcal{F}_a(t) 为驱动函数。

信息墙影响函数#

  1. 效价驱动函数:
Fv(t)=[(1−q)hiv(t)+qhmfv(t)]⋅[c1+c2(vi(t)−vi3(t))]⋅[1−∣vi(t)∣] \mathcal{F}_v(t) = [(1-q)h_i^v(t) + qh_{mf}^v(t)] \cdot [c_1 + c_2(v_i(t) - v_i^3(t))] \cdot [1 - \lvert v_i(t) \rvert]
  1. 唤醒度驱动函数:
Fa(t)={(1−q)[ϵhia(t)+(1−ϵ)h‾ia(t)]+qhmfa(t)}[1−ai(t)]\mathcal{F}_a(t) = \{(1-q)[\epsilon h_i^a(t) + (1-\epsilon)\overline{h}_i^a(t)] + qh_{mf}^a(t)\}[1 - a_i(t)]

说明:
情绪越极端，响应外部刺激的程度越弱。
当 vi(t)→0v_i(t) \to 0 时影响最大，vi(t)→±1v_i(t) \to \pm 1 时影响趋近 0。

活跃状态 e (0 或 1)#

活跃状态由 MySpace 时间钟模型控制。

三类聚合情绪信息#

1. 自身墙信息 hiz(t)h_i^z(t)（包括 hiv(t),hia(t)h_i^v(t), h_i^a(t)#

hiz(t)=∑j∑m∈Mjiθ(t,tm)zj(tm)Wjie−γh(tjilm−tm)∑j∑m∈Mjiθ(t,tm)Wjie−γh(tjilm−tm)e−γh(t−tjilm)h_{i}^{z}(t) = \frac{\sum_{j}\sum_{m\in M_{ji}}\theta(t,t_{m})z_{j}(t_{m})W_{ji}e^{-\gamma^{h}(t_{ji}^{lm}-t_{m})}}{\sum_{j}\sum_{m\in M_{ji}}\theta(t,t_{m})W_{ji}e^{-\gamma^{h}(t_{ji}^{lm}-t_{m})}}e^{-\gamma^{h}(t-t_{ji}^{lm})}

说明:

  • zz 表示 vv 或 aa
  • θ(t,tm)\theta(t,t_m) 是阶梯函数，确保消息生效期
  • WjiW_{ji} 为边权
  • γh\gamma^h 为信息衰减率

2. 朋友墙信息 h‾ia(t)\overline{h}_i^a(t)#

h‾ia(t)=∑jWijhja(t)(1+hjv(t)vi(t))∑jWij(1+hjv(t)vi(t))\overline{h}_{i}^{a}(t) = \frac{\sum_{j}W_{ij}h_{j}^{a}(t)(1+h_{j}^{v}(t)v_{i}(t))}{\sum_{j}W_{ij}(1+h_{j}^{v}(t)v_{i}(t))}

其中 WijW_{ij} 为好友关系强度,若 vj(t)v_j(t) 和 vi(t)v_i(t) 越一致，情绪影响越强

3. 平均场信息 hmfz(t)h_{mf}^z(t)#

表示整个社区情绪的聚合。

情绪更新规则#

  1. vv 受 hiv(t)h_i^v(t) 影响，aa 受 hiv(t),hia(t),h‾ia(t)h_i^v(t), h_i^a(t), \overline{h}_i^a(t) 联合影响
  2. 外部刺激模拟为情绪重置（以概率 P0P_0 出现）
  3. 若无信息刺激，v,a→0v, a \to 0

消息传播机制#

消息发送#

  • 节点需处于活跃状态
  • 消息内容为 (v,a)(v, a)
  • 发送概率为:ai(t)⋅Pa_i(t) \cdot P

发送人选择依据:

hjia(t)=∑m∈MjiΘ(t,tm)aj(tm)e−γh(tjilm−tm)∑m∈MjiΘ(t,tm)e−γh(tjilm−tm)e−γh(t−tjilm)h_{ji}^{a}(t)=\frac{\sum_{m\in M_{ji}}\Theta(t,t_{m})a_{j}(t_{m})e^{-\gamma^{h}(t_{ji}^{lm}-t_{m})}}{\sum_{m\in M_{ji}}\Theta(t,t_{m})e^{-\gamma^{h}(t_{ji}^{lm}-t_{m})}}e^{-\gamma^{h}(t-t_{ji}^{lm})}

消息选择权重:

sj(t)=ω′[βWijhjia(t)∑kWik+(1−β)Wjihjia(t)(1+hjv(t)vi(t))∑kWik(1+hkv(t)vi(t))]s_{j}(t) = \omega^{\prime} \left[ \beta \frac{W_{ij}h_{ji}^{a}(t)}{\sum_{k}W_{ik}} + (1-\beta) \frac{W_{ji}h_{ji}^{a}(t)(1+h_{j}^{v}(t)v_{i}(t))}{\sum_{k}W_{ik}(1+h_{k}^{v}(t)v_{i}(t))} \right]

消息接受#

  • 接收者将消息放入自身情绪墙并更新其状态

模型运行流程#

  1. 每个代理计算 v,av, a 的更新值
  2. 按概率对部分代理执行“情绪重置”
  3. 判断哪些用户在线+活跃
  4. 对活跃用户:
    • 更新其情绪列表
    • 执行消息发送操作

实验结果#

模拟 vs 实际数据对比#

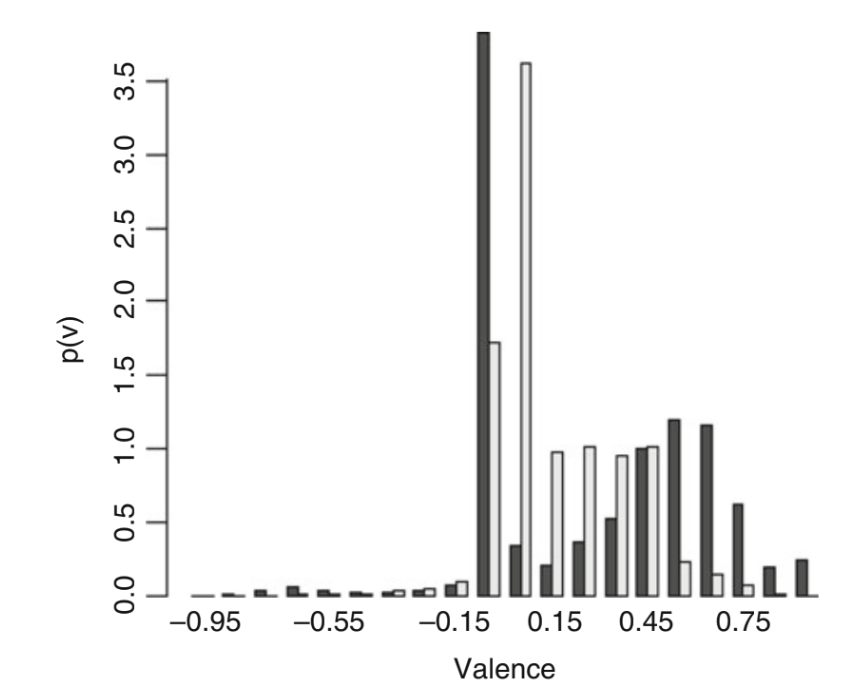
深色:真实数据
灰色:模拟情绪
可以看到两者的趋势基本一致，具有相同单调性和分布结构。

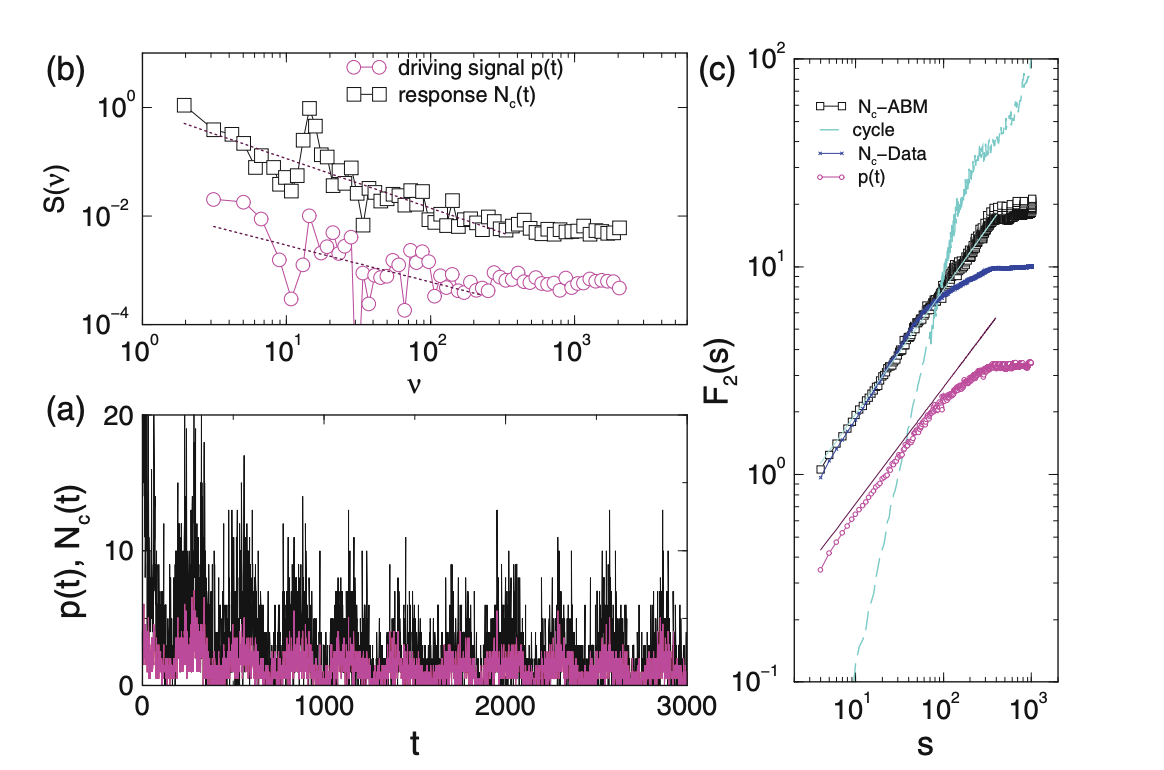
斜率范围在 [0.5,1][0.5, 1]，说明具有长期相关性。
当时间尺度 ss 增大时，真实数据和模拟数据斜率一致。
对照实验 clcle 表明:若无外部事件，集体情绪不会产生长期趋势。
因此，集体情绪的形成不是随机的，而是具有持续影响性的。

评论