返回首页

生成式对抗网络(GAN)--相关文献调研

2025-07-12 暑假 科研
2245 字 11 分钟
生成式对抗网络(GAN)--相关文献调研
目录 ⌄
内容时效性提醒

"本篇博客完成日期距现在已大于一年，内容可能已过时，相关技术、政策或情况可能已发生变化，建议读者查证最新信息。"

对抗生成网络#

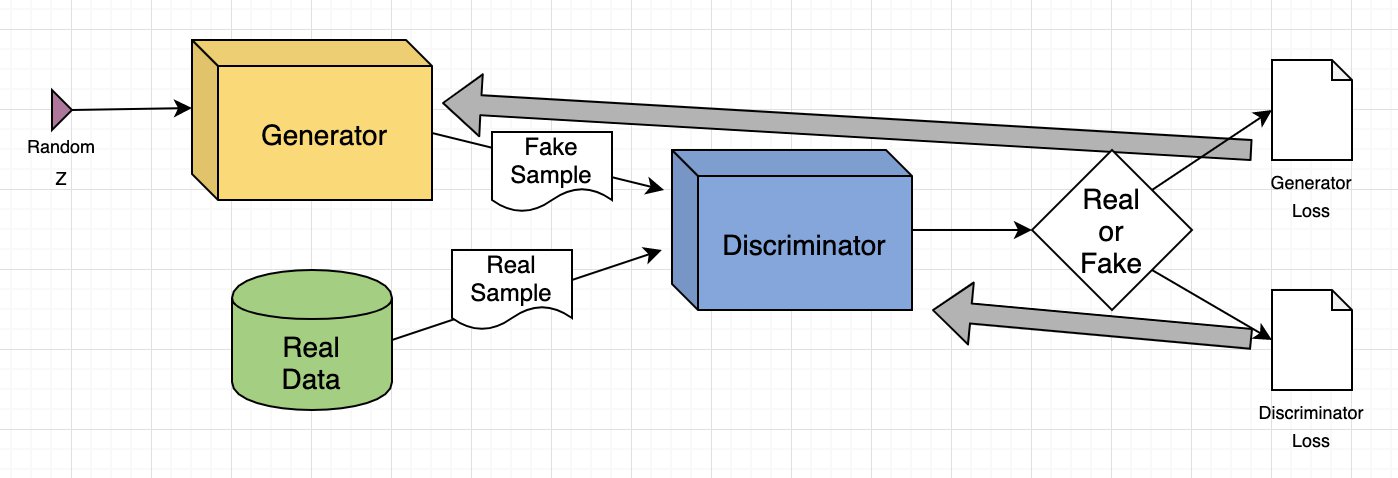
模型结构#

  1. 生成模型 G: 捕捉数据分布
  2. 判别模型 D: 估计样本来自训练数据还是 G的概率(判别是真的还是假的的概率)

训练方式#

数据要求: 以张量的形式传入[M, N, K]

  1. 基于反向传播机制
minGmaxDV(D,G)=Ex∼pdata(x)[log⁡D(x)]+Ez∼pz(z)[log⁡(1−D(G(z)))]min_G max_D V(D,G) = E_{x \sim p_{data}(x)}[\log D(x)] + E_{z \sim p_z(z)}[\log(1-D(G(z)))]

  • 判别器 D 的目标maxDV(D,G)→Ex∼pdata(x)[log⁡D(x)]+Ez∼pz(z)[log⁡(1−D(G(z)))]max_DV(D,G) \rightarrow E_{x \sim p_{data}(x)}[\log D(x)] + E_{z \sim p_z(z)}[\log(1-D(G(z)))]

  • 生成器 G 的目标就是最小化 D 的目标价值,→minG(maxDV(D,G))\rightarrow min_G(max_DV(D,G))

  • 在实际G的模型训练中,由于一开始的生成网络与实际网络差异大,D(G(z))D(G(z)) 更趋向于 0,所以 G难以从 判别器D中获得梯度信号,难以改进生成能力,所以训练G时,可以最大化(logD(G(z)))

训练机制#

交替进行 k步 D优化, 一步G优化

  1. 训练判别器 D

1.1 批量训练的平均损失函数

1m∑i=1m[log⁡D(x(i))+log⁡(1−D(G(z(i))))]\frac{1}{m}\sum_{i=1}^{m}[\log D(x^{(i)})+\log(1-D(G(z^{(i)})))]

1.2 梯度计算

∇θd1m∑i=1m[log⁡D(x(i))+log⁡(1−D(G(z(i))))]\nabla_{\theta_d} \frac{1}{m}\sum_{i=1}^{m}[\log D(x^{(i)})+\log(1-D(G(z^{(i)})))]

1.3 参数更新

θd←θd+α∇θdLD\theta_d \leftarrow \theta_d + \alpha \nabla_{\theta_d} L_D

LDL_D 是判别器的损失函数,α\alpha 是学习率

  1. 训练生成器 G **原始目标:最小化 log(1−D(G(z))→log(1- D(G(z)) \rightarrow 最大化 log(D(G(z)))log(D(G(z))) **

2.1 批量训练的平均损失函数

1m∑i=1m[log(1−D(G(Z(i))))] \frac{1}{m} \sum_{i = 1}^{m}[log(1 - D(G(Z^{(i)})))]

2.2 梯度计算

∇θd1m∑i=1m[log(1−D(G(zi))] \nabla_{\theta_d} \frac{1}{m} \sum_{i = 1}^{m}[log(1 - D(G(z^{i}))]

2.3 参数更新

θg←θg−α∇θgLG \theta_g \leftarrow \theta_g - \alpha \nabla_{\theta_g}L_G

注意: 进行 G更新的时候,判别器 D的参数是冻结的

CycleGAN#

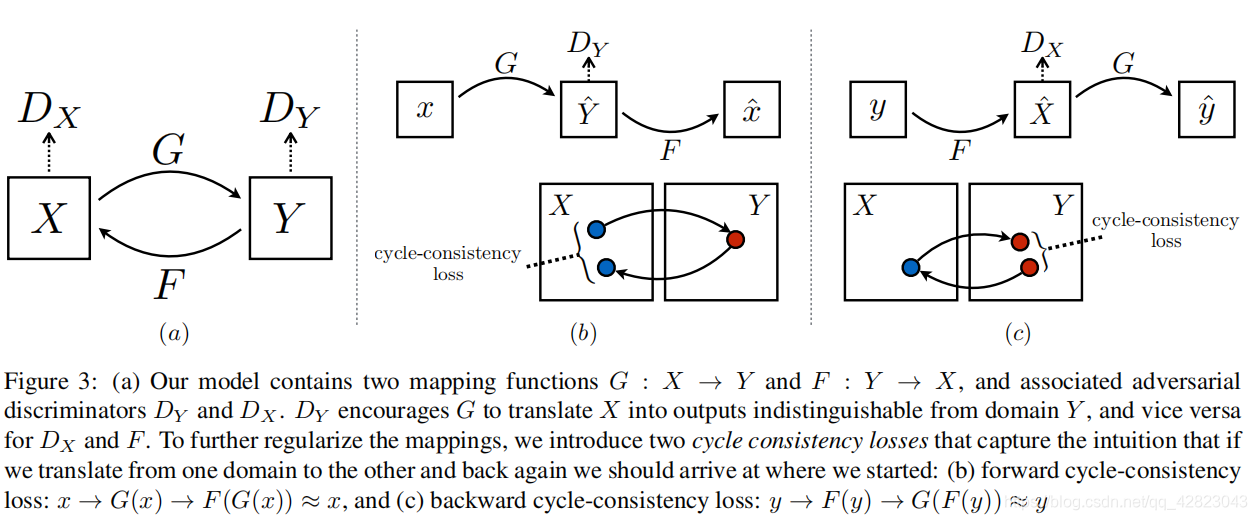
模型结构#

  1. 两个生成模型 G 和 F:

    • 生成器 G: 学习将图像从域 X 转换到域 Y 的映射，即 G:X→YG: X \rightarrow Y
    • 生成器 F: 学习将图像从域 Y 转换到域 X 的映射，即 F:Y→XF: Y \rightarrow X

  2. 两个判别模型 DXD_X 和 DYD_Y:

    • 判别器 DYD_Y: 区分图像是来自目标域 Y 的真实图像还是由 G 生成的假图像 G(x)G(x)
    • 判别器 DXD_X: 区分图像是来自目标域 X 的真实图像还是由 F 生成的假图像 F(y)F(y)

训练方式#

CycleGAN的训练目标是学习两个映射 GG 和 FF，使得:

  • G(x)G(x) 的图像与域 Y 中的图像无法区分
  • F(y)F(y) 的图像与域 X 中的图像无法区分

为了实现无监督训练,提出了循环一致性损失（Cycle Consistency Loss）

  • 前向循环一致性: x→G(x)→F(G(x))≈xx \rightarrow G(x) \rightarrow F(G(x)) \approx x
  • 后向循环一致性: y→F(y)→G(F(y))≈yy \rightarrow F(y) \rightarrow G(F(y)) \approx y

整个优化目标函数是对抗性损失（Adversarial Loss）和循环一致性损失的加权和

联合损失函数#
L(G,F,DX,DY)=LGAN(G,DY,X,Y)+LGAN(F,DX,Y,X)+λLcyc(G,F)\mathcal{L}(G, F, D_X, D_Y) = \mathcal{L}_{GAN}(G, D_Y, X, Y) + \mathcal{L}_{GAN}(F, D_X, Y, X) + \lambda \mathcal{L}_{cyc}(G, F)

其中 λ\lambda 是循环一致性损失的权重

1. 对抗性损失 (Adversarial Loss)#

CycleGAN 使用标准的 GAN 损失来提高生成的图像与目标域中的图像分布匹配准确率

1.1 生成器 G 和 判别器 DYD_Y 的对抗损失: 鼓励 G(x)G(x) 看起来像真实图像 Y

LGAN(G,DY,X,Y)=Ey∼pdata(y)[log⁡DY(y)]+Ex∼pdata(x)[log⁡(1−DY(G(x)))] \mathcal{L}_{GAN}(G, D_Y, X, Y) = E_{y \sim p_{data}(y)}[\log D_Y(y)] + E_{x \sim p_{data}(x)}[\log(1-D_Y(G(x)))]

相关概念

  • 判别器 DYD_Y 的目标是最大化 LGAN(G,DY,X,Y)\mathcal{L}_{GAN}(G, D_Y, X, Y)

  • 生成器 G 的目标是最小化 LGAN(G,DY,X,Y)\mathcal{L}_{GAN}(G, D_Y, X, Y)

  • G 通常会最大化 Ex∼pdata(x)[log⁡DY(G(x))]E_{x \sim p_{data}(x)}[\log D_Y(G(x))] 以避免早期训练不稳定。

    1.2 生成器 F 和 判别器 DXD_X 的对抗损失: 鼓励 F(y)F(y) 看起来像真实图像 X

LGAN(F,DX,Y,X)=Ex∼pdata(x)[log⁡DX(x)]+Ey∼pdata(y)[log⁡(1−DX(F(y)))] \mathcal{L}_{GAN}(F, D_X, Y, X) = E_{x \sim p_{data}(x)}[\log D_X(x)] + E_{y \sim p_{data}(y)}[\log(1-D_X(F(y)))]

相关概念

  • 判别器 DXD_X 的目标是最大化 LGAN(F,DX,Y,X)\mathcal{L}_{GAN}(F, D_X, Y, X)
  • 生成器 F 的目标是最小化 LGAN(F,DX,Y,X)\mathcal{L}_{GAN}(F, D_X, Y, X)
  • 在实际训练中，F 通常会最大化 Ey∼pdata(y)[log⁡DX(F(y))]E_{y \sim p_{data}(y)}[\log D_X(F(y))]
2. 循环一致性损失 (Cycle Consistency Loss)#

循环一致性损失确保了转换的可逆性，防止生成器学习到将源域中的所有图像映射到目标域中的相同图像，从而避免“模式崩溃”,就是降低泛化能力

2.1 前向循环一致性损失:

Lcyc(G,F)=Ex∼pdata(x)[∣∣F(G(x))−x∣∣1] \mathcal{L}_{cyc}(G, F) = E_{x \sim p_{data}(x)}[||F(G(x)) - x||_1]

2.2 后向循环一致性损失:

Lcyc(G,F)=Ey∼pdata(y)[∣∣G(F(y))−y∣∣1] \mathcal{L}_{cyc}(G, F) = E_{y \sim p_{data}(y)}[||G(F(y)) - y||_1]

常见使用 L1 范数 (∣∣⋅∣∣1||\cdot||_1) 来计算循环一致性损失

训练机制#

CycleGAN 的训练也采用交替优化策略，同时优化两个生成器和两个判别器

  1. 训练判别器 DXD_X 和 DYD_Y: 对于 DYD_Y: 使用来自域 Y 的真实图像 yy 和由 G 生成的假图像 G(x)G(x) 来计算损失并更新参数 批量训练的平均损失函数（以 DYD_Y 为例，目标是最大化）: 1m∑i=1m[log⁡DY(y(i))+log⁡(1−DY(G(x(i))))] \frac{1}{m}\sum_{i=1}^{m}[\log D_Y(y^{(i)})+\log(1-D_Y(G(x^{(i)})))]

1.1 梯度计算:

∇θDY1m∑i=1m[log⁡DY(y(i))+log⁡(1−DY(G(x(i))))] \nabla_{\theta_{D_Y}} \frac{1}{m}\sum_{i=1}^{m}[\log D_Y(y^{(i)})+\log(1-D_Y(G(x^{(i)})))]

1.2 参数更新:

θDY←θDY+α∇θDYLGAN(G,DY,X,Y) \theta_{D_Y} \leftarrow \theta_{D_Y} + \alpha \nabla_{\theta_{D_Y}} \mathcal{L}_{GAN}(G, D_Y, X, Y)

1.3 对于 DXD_X: 类似地，使用来自域 X 的真实图像 xx 和由 F 生成的假图像 F(y)F(y) 来计算损失并更新参数

  1. 训练生成器 G 和 F: 对于 G 和 F: 计算包括对抗损失和循环一致性损失在内的总损失 * 批量训练的平均损失函数（以 G 为例，目标是最小化其对抗部分，并最小化循环一致性部分）:
1m∑i=1m[−log⁡DY(G(x(i)))]+λ1m∑i=1m[∣∣F(G(x(i)))−x(i)∣∣1] \frac{1}{m}\sum_{i=1}^{m}[-\log D_Y(G(x^{(i)}))] + \lambda \frac{1}{m}\sum_{i=1}^{m}[||F(G(x^{(i)})) - x^{(i)}||_1]

2.1 梯度计算:

∇θG(1m∑i=1m[−log⁡DY(G(x(i)))]+λ1m∑i=1m[∣∣F(G(x(i)))−x(i)∣∣1]) \nabla_{\theta_G} \left( \frac{1}{m}\sum_{i=1}^{m}[-\log D_Y(G(x^{(i)}))] + \lambda \frac{1}{m}\sum_{i=1}^{m}[||F(G(x^{(i)})) - x^{(i)}||_1] \right)

2.2 参数更新:

θG←θG−α∇θGLtotal \theta_G \leftarrow \theta_G - \alpha \nabla_{\theta_G} \mathcal{L}_{total}

注意: 进行 G 和 F 更新时，判别器 DXD_X 和 DYD_Y 的参数是冻结的

DCGAN#

Pytorch代码库

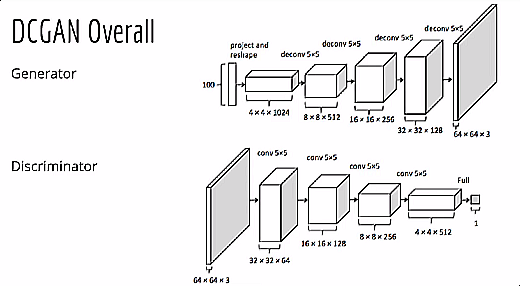
摘要翻译#

以下是该论文摘要部分的翻译: 近年来，使用卷积网络（CNNs）的监督学习在计算机视觉应用中得到了广泛的应用 。相比之下，使用CNNs的无监督学习受到的关注较少 。在这项工作中，我们希望能帮助缩小CNNs在监督学习和无监督学习方面成功应用之间的差距 。我们引入了一类名为深度卷积生成对抗网络（DCGANs）的CNN，它们具有特定的架构约束，并证明了它们是无监督学习的有力候选者 。通过在各种图像数据集上进行训练，我们展示了令人信服的证据，表明我们的深度卷积对抗对（deep convolutional adversarial pair）在生成器和判别器中都学习到了从对象部分到场景的层次化表示 。此外，我们将学习到的特征用于新颖的任务——展示了它们作为通用图像表示的适用性 。

研究方法#

提出 深度卷积GANs(DCGAN),其实就是针对于 生成器和判别器两个神经网络进行结构调整,将全连接网络改成CNN卷积神经网络

  1. 用跨步卷积(判别器)和分数步长卷积(生成器)替换所有池化层

  2. 在生成器和判别器中都使用批量归一化(batchnorm)

  3. 对于更深层的架构，移除全连接隐藏层

  4. 在生成器中，除使用Tanh的输出层外，所有层都使用ReLU激活函数

  5. 在判别器中，所有层都使用LeakyReLU激活函数

StyleGAN#

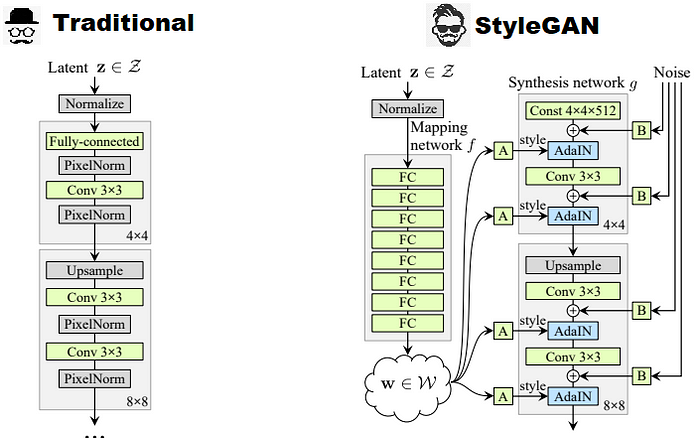
摘要翻译#

我们为生成对抗网络（GANs）提出了一种替代性的生成器架构，该架构借鉴了风格迁移领域的文献。 这种新架构能够自动地、无监督地将高层级属性（例如，在人脸数据上训练时学到的姿态和身份）与生成图像中的随机变化（例如，雀斑、头发）分离开来。同时，它还实现了对合成过程直观的、特定尺度的控制。 在传统的分布质量指标方面，新的生成器提升了当前顶尖水平（state-of-the-art）的表现，并展现出更好的插值特性，也能更好地解耦变化的潜在因子。为了量化插值质量和解耦程度，我们提出了两种新的、适用于任何生成器架构的自动化评估方法。 最后，我们引入了一个全新的、高度多样化且高质量的人脸数据集。

研究方法#

针对于 GAN的生成器的结构进行改良

  1. 将随机噪声 Z 输入 Mapping network(非线形映射网络f:Z→Wf: Z \rightarrow W，通过 MLP多层感知机实现) 中,将 Z 转化为 W,W 在第k层通过仿射变换形成(ys,k,yb,ky_{s,k},y_{b,k}),影响每一层的特征值归一化
  2. 对每一个通道的特征向量进行归一化 相关概念: 将 Z→WZ \rightarrow W 将Z(存在属性纠缠)转化到 W空间,更容易找到图像的独立属性
AdaIN(x,y)=ys,ixi−μ(xi)σ(xi)+yb,i(1)\text{AdaIN}(\mathbf{x}, \mathbf{y}) = \mathbf{y}_{s,i} \frac{\mathbf{x}_i - \mu(\mathbf{x}_i)}{\sigma(\mathbf{x}_i)} + \mathbf{y}_{b,i} \quad (1)

相关概念:

  • W 专门化分为风格 y=(ys,yb)y = (y_s, y_b)
  • xix_i 表示每一个通道的特征值

WGAN#

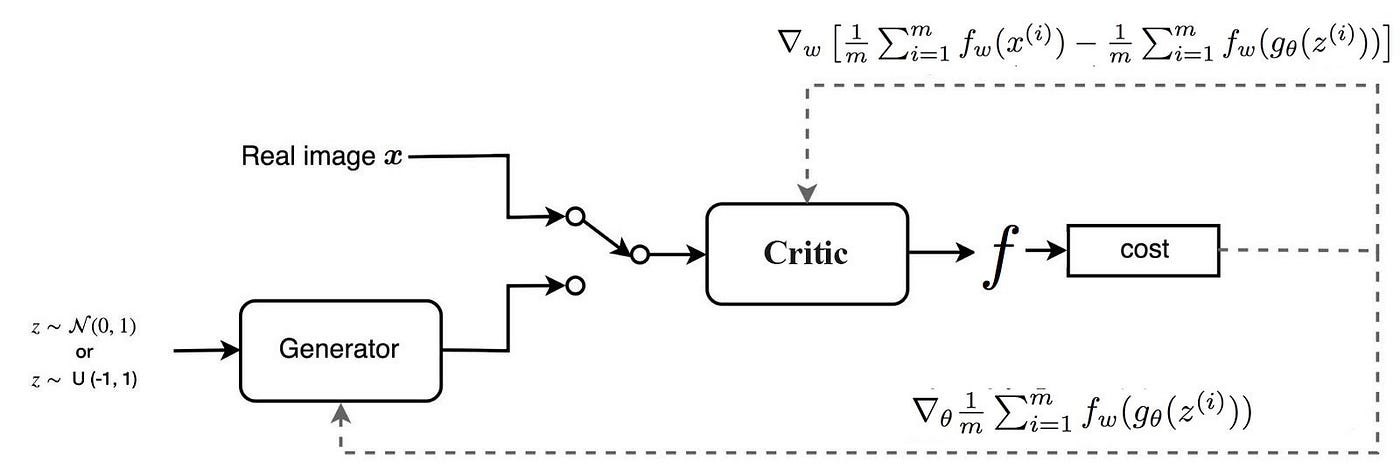
研究方法#

修改了 传统的GAN的损失函数

总体的损失函数#

min⁡gθmax⁡fw∈FL(Ex∼Pr[fw(x)]−Ez∼p(z)[fw(gθ(z))])\min_{g_{\theta}} \max_{f_w \in \mathcal{F}_L} \left( \mathbb{E}_{x \sim \mathbb{P}_r}[f_w(x)] - \mathbb{E}_{z \sim p(z)}[f_w(g_{\theta}(z))] \right)

判别器损失函数 LDL_D#

LD=Ex∼Pr[fw(x)]−Ez∼p(z)[fw(gθ(z))](3)L_D = \mathbb{E}_{x \sim \mathbb{P}_r}[f_w(x)] - \mathbb{E}_{z \sim p(z)}[f_w(g_{\theta}(z))] \quad (3)

相关概念

  • fwf_w是判别器网络(神经网络),实际上是 Earth Mover(EM)距离,可以理解为会识别这个数据和真实数据的相似程度,有一个上界K

生成器损失函数 LGL_G#

LG=−Ez∼p(z)[fw(gθ(z))]L_G = -\mathbb{E}_{z \sim p(z)}[f_w(g_{\theta}(z))]

评论