暑假闲事-基础技能

25 年 8 月 3 日 星期日 (已编辑)
1280 字
7 分钟

神经网络与pytorch入门

神经网络

可视化网站

核心优化公式:

L=min(F(θ))L = min(F(\theta))

使用方法: 梯度下降法(往最快下降的方向走一步)

针对于这个部分才是我需要研究的重点,由于在多层神经网络中,梯度的计算决定了参数的调整,也能让我们更好的了解神经网络的细节内容

θi+1=θi+Δθi\theta_{i + 1} = \theta_i + \Delta\theta_i

从而得到:

Δθi=−dfdθ\Delta\theta_i = -\frac{df}{d\theta}

怎么计算梯度(BP算法--反向传播算法)

[!TIP] 通过链式法则调整计算梯度,调整模型参数

  1. 前向传播:计算输出值
  2. 损失计算:预测值和真实标签计算损失
  3. 反向传播:根据层级计算梯度,逐层传播误差
  4. 权重更新:使用梯度下降法更新权重 如果我要计算每一层的可训练参数 W(举例),我需要计算他和 结果的梯度关系来进行参数调整 ∂J∂W(1)=prod(∂J∂z,∂z∂W(1))+prod(∂J∂s,∂s∂W(1))=frac∂J∂zxT+γWT\frac{\partial J}{\partial W^{(1)}} = prod(\frac{\partial J}{\partial z}, \frac{\partial z}{\partial W^{(1)}}) + prod(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial W^{(1)}}) = frac{\partial J}{\partial z}x^{T} + \gamma W^{T}

Pytorch入门

Autograd:自动微分

  1. 计算图:一系列节点和边组成的有向无环图,节点表示一个操作或者变量,边表示变量之间的依赖关系
  2. 在对张量执行操作的时候,pytorch会创建一个新的计算图节点,记录该操作以及他的输入输出:操作-输入张量-输出张量
  3. 查看计算图: 可视化库(Graphviz)

LLM Reasoning

[!WARNRING] 听不懂,纯科普类😓

自然语言处理与主流LLM架构

前置知识

  1. Softmax函数

    [!TIP] 类似于归一化的的操作,变成概率的形式

Softmax(zi)=exp(zi)∑jexp(zi)Softmax(z_i) = \frac{exp(z_i)}{\sum_{j}exp(z_i)}
  1. 全连接层

    [!TIP] 每一个神经元都与上一层的所有节点输出

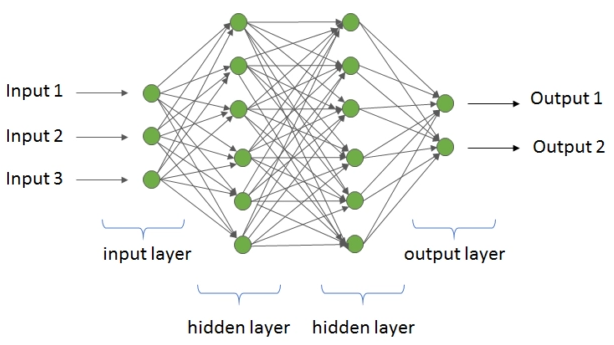
  1. 激活函数

    [!TIP] 将输出转化为非线性化(输出是线性的,不能处理非线性任务)

常用激活函数

,Sigmod,ELU

  1. 残差连接

    [!TIP] 中间激活值跳过某些神经网络层,防止梯度消失的问题,让梯度能更好的回传

Transformer And Attention

  1. Word Embedding (词嵌入) 将词语转化为 d维稠密向量,单词在多维空间中的距离突出了两者之间的关系强度

  2. Self-Attention(自注意理机制) 简单的 Attention 机制: 设置一个注意力矩阵,突出

图片展示

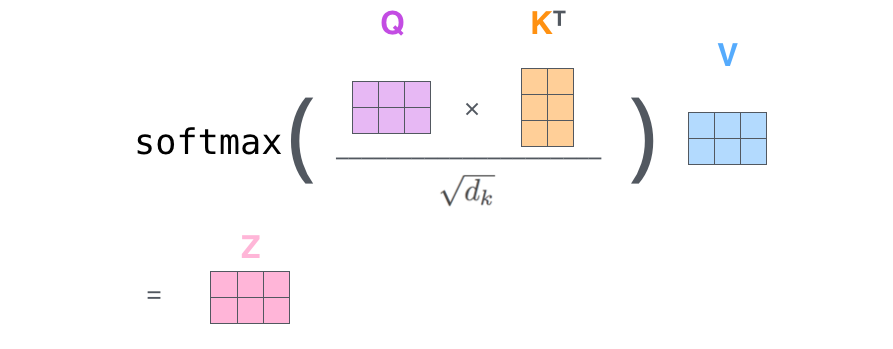
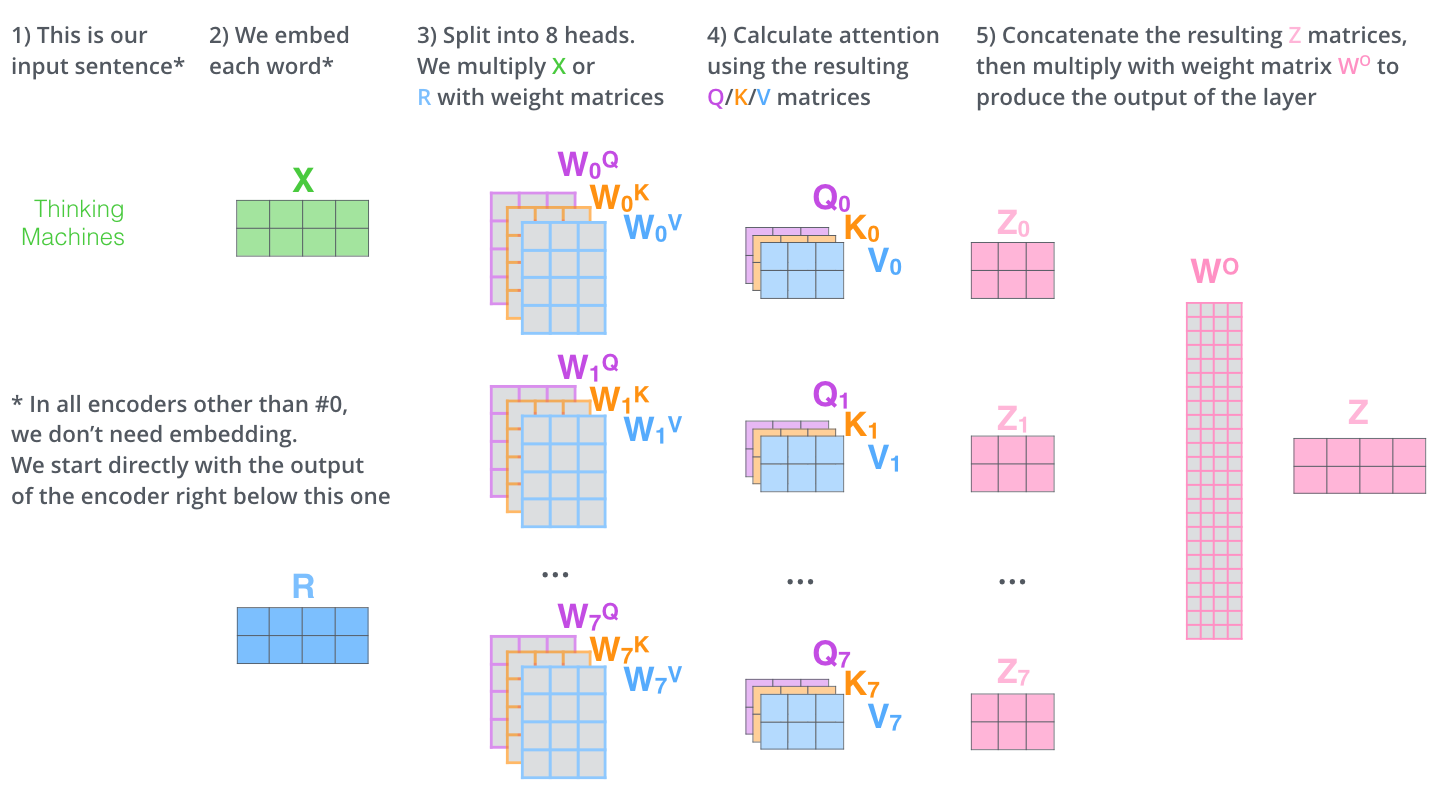
  1. Masked Multi-Head Attention 要求输出的时候,某个词语只能注意到它前面已经生成的词语,设计了Mask矩阵
  1. Position Encoding

    [!TIP] Attention 机制没有考虑向量在 sequence 中的位置

设置函数 F,输入 词位置和 word embedding

F(pos,embedding)=DEmbeggingandpositionF(pos, embedding) = D_{Embegging_and_position}

  1. 前馈层 一个两层的全连接层,第一层是 relu 激活

    max(0,XW1+b1)W2+b2max(0, XW_1 + b_1)W_2 + b_2

  2. add & norm

    1. add表示残差连接,缓解梯度消失
LayerNorm(X+MultiHeadAttention(X))LayerNorm(X + MultiHeadAttention(X))
  1. norm 表示 通过归一化每一层中每个样本的特征值,提高模型训练的稳定性
y=x−E(x)Var(x)+θ∗γ+βy = \frac{ x - E(x) }{ \sqrt{Var(x) + \theta} } *\gamma + \beta

图神经网络

相关作用

  1. 节点级别任务
  • 节点分类
  • 节点位置优化
  1. 边级别任务
  • 预测节点之间关系
  1. 图级别任务
  • 图分类任务
  • 图性质预测

基础知识

对嵌入向量进行学习更新(图神经网络)

  1. 顶点特征嵌入 ViV_i
  2. 边特征嵌入 EiE_i
  3. 全局特征嵌入 UU

toy GNN(最简单神经网络迭代形式)

Vil+1=MLPVl(Vil),Eil+1=MLPEl(Eil),Uil+1=MLPUl(Uil)V_i^{l + 1} = MLP_V^{l}(V_i^l),E_i^{l + 1} = MLP_E^{l}(E_i^l),U_i^{l + 1} = MLP_U^{l}(U_i^l)

GCN(图卷积网络)

为了学习节点之间的关系,利用到图的信息 核心传递公式:

H(l+1)=σ(AH(l)W(l))H^{(l + 1)} = \sigma(AH^{(l)}W^{(l)})

相关概念:

  • A 归一化后的邻接矩阵 A = D−12A′D−12D^{-\frac{1}{2}} A' D^{-\frac{1}{2}}
  • W可训练参数矩阵
  • H表示节点的特征矩阵

example:

Vil=Vil+∑tVtl,Vil=σ(Vil)V_i^l = V_i^l + \sum_{t}V_t^l,V_i^l = \sigma{(V_i^l)}

相关性质:

  • 消息聚合操作不一定要加法,也可以是加权求和,取平均
  • K层GCN,就表示顶点可以聚合它k步以内的节点信息

GAT(图注意力网络)

一层计算（单头）

给定节点特征 (H∈RN×F)(\mathbf{H}\in\mathbb{R}^{N\times F})

  1. 线性变换 hi′=Whi,W∈RF′×F\mathbf{h}_i'=\mathbf{W}\mathbf{h}_i,\quad \mathbf{W}\in\mathbb{R}^{F'\times F}
  2. 注意力打分（未归一化）（对每条边 (i\leftrightarrow j)） eij=LeakyReLU ⁣(a⊤[hi′ ∥ hj′]),a∈R2F′e_{ij}=\mathrm{LeakyReLU}\!\left(\mathbf{a}^\top[\mathbf{h}_i'\,\Vert\,\mathbf{h}_j']\right),\quad \mathbf{a}\in\mathbb{R}^{2F'} 相关概念:
  • ∥\Vert 表示将向量拼接

  1. Softmax 归一化（对同一接收节点 (i) 的邻居集合 (\mathcal{N}(i))）

    αij=exp⁡(eij)∑k∈N(i)exp⁡(eik)\alpha_{ij}=\frac{\exp(e_{ij})}{\sum_{k\in\mathcal{N}(i)}\exp(e_{ik})}

  2. 加权聚合 + 激活

$$ \mathbf{h}_i^{\text{out}}=\sigma\!\left(\sum_{j\in\mathcal{N}(i)}\alpha_{ij}\,\mathbf{h}_j'\right) $$

多头注意力（Multi-Head）

  • 中间层（拼接）
$$ \mathbf{h}_ i^{\text{out}}=\big\Vert_{m=1}^M \sigma\!\left(\sum_{j}\alpha_{ij}^{(m)}\,\mathbf{W}^{(m)}\mathbf{h}_j\right) $$
- **最后一层（平均）**
$$ \mathbf{h}_i^{\text{out}}=\frac{1}{M}\sum_{m=1}^M \sigma\!\left(\sum_{j}\alpha_{ij}^{(m)}\,\mathbf{W}^{(m)}\mathbf{h}_j\right) $$

E(n) 等变图神经网络

相关性质

  1. 等变性

    f(Tg(x))=Tg′(f(x))f(T_g(x)) = T'_g(f(x))

  2. 不变性

    f(T(x))=f(x)f(T(x)) = f(x)

核心公式

[!TIP] 其实就是加入了节点之间的距离(是多维距离)信息

给定节点特征 (hi)(h_i)、坐标 (xi)(x_i)、（可选）边特征 (aij)(a_{ij}):

$$ \begin{aligned} m_{ij} &= \phi_m\!\big(h_i,\,h_j,\,\|x_i-x_j\|^2,\,a_{ij}\big)\quad\\ x_i' &= x_i + \sum_{j\in\mathcal N(i)} \underbrace{\phi_x(m_{ij})}(x_i-x_j) \\ h_i' &= \phi_h\!\Big(h_i,\, \sum_{j} m_{ij}\Big) \end{aligned} $$
- 仅使用**距离**与**方向**（而非绝对坐标），从而对平移/旋转/反射保持 E(n) 等变。

GNN的过平滑问题

图的连通性问题,随着多层信息聚合,邻居信息会覆盖掉自身信息,

解决办法:

  1. Dropout: 训练过程中随机丢弃一些神经元

文章标题：暑假闲事-基础技能

文章作者：jiely

文章链接：https://whalefall.top/posts/2025-08-03-basical-knowledge[复制]

最后修改时间：

商业转载请联系站长获得授权，非商业转载请注明本文出处及文章链接，您可以自由地在任何媒体以任何形式复制和分发作品，也可以修改和创作，但是分发衍生作品时必须采用相同的许可协议。
本文采用CC BY-NC-SA 4.0进行许可。