weka实现降维,分类,聚类
2023-08-09 14:53:19 # Big Data # weka

实验使用java weka api，首先导入weka依赖

1
2
3
4
5
6
<!-- https://mvnrepository.com/artifact/nz.ac.waikato.cms.weka/weka-stable -->
<dependency>
    <groupId>nz.ac.waikato.cms.weka</groupId>
    <artifactId>weka-stable</artifactId>
    <version>3.8.6</version>
</dependency>

1.降维

1.1 方法介绍

数据降维采用PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。

PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n条这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k条坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k条含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

1.2 代码实现

1
2
3
4
5
6
7
8
9
10
11
try {
	Instances dataset = DataSource.read("src/main/resources/diabetes.arff");
    dataset.setClassIndex(dataset.numAttributes() - 1);

    PrincipalComponents pca = new PrincipalComponents();
    pca.setCenterData(true);
    pca.buildEvaluator(dataset);
    System.out.println(pca);
} catch (Exception e) {
    e.printStackTrace();
}

首先通过DataSource读取数据集，设置最后一列为标签(setClassIndex),然后创建PrincipalComponents对象，设置对数据进行中心化处理，随后导入数据，初始化主成分并执行分析，最后打印结果即可

1.3 实验结果

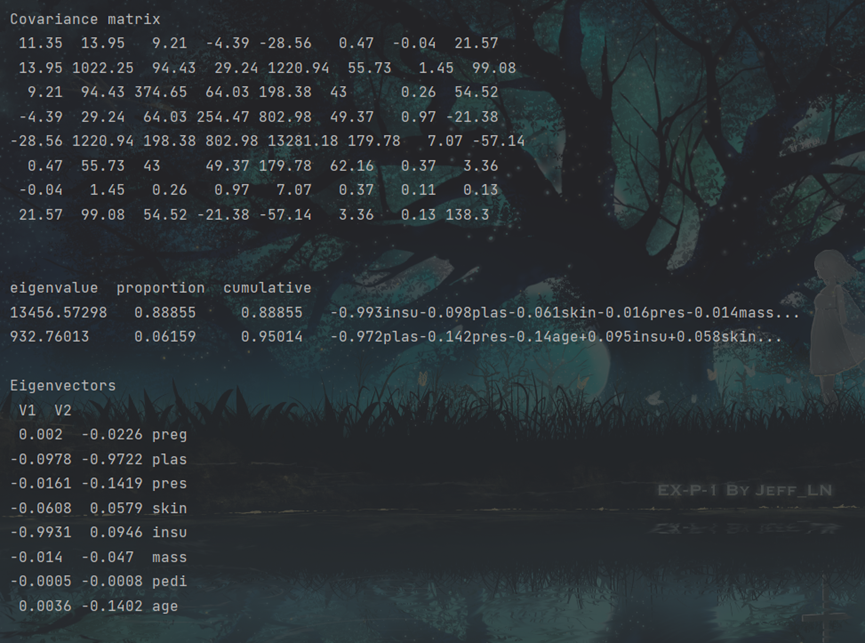
image-20221013003759127

计算出的协方差矩阵如图所示，可以看到原本为八维的数据被降为二维，效果显著

2.分类

2.1 方法介绍

分类采用J48实现，J48是基于从上到下的策略，递归的分治策略，选择某个属性放置在根节点，为每个可能的属性值产生一个分支，将实例分成多个子集，每个子集对应一个根节点的分支，然后在每个分支上递归地重复这个过程。当所有实例有相同的分类时停止。

2.2 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
try {
	Instances data = DataSource.read("src/main/resources/spambase.train.arff");
    Instances test_data = DataSource.read("src/main/resources/spambase.test.arff");
    data.setClassIndex(data.numAttributes() - 1);
    test_data.setClassIndex(test_data.numAttributes() - 1);
    Instance test_instance = test_data.firstInstance();
    J48 j48 = new J48();
    j48.buildClassifier(data);
	System.out.println(j48);
    System.out.println(j48.classifyInstance(test_instance));
} catch (Exception e) {
    e.printStackTrace();
}

首先通过DataSource读取训练数据集以及测试数据集，设置最后一列为标签(setClassIndex),再获取测试数据集中的测试数据，然后创建J48对象，随后导入数据，生成分类器，最后打印分类器信息以及对测试数据进行分类的结果

2.3 实验结果

可以看到J48生成的决策树，以及树的大小和叶子数，以及测试数据分类后的结果

image-20221013004059857

image-20221013004106306

3.聚类

3.1 方法介绍

聚类采用K-means实现，K-Means算法是一种聚类分析的算法。首先从样本中随机选择k个点作为初始质心，随后计算每个样本到各个质心的距离，将样本划分到距离最近的质心所对应的簇中，计算每个簇中所有样本的均值，并使用该均值更新簇的质心，重复以上步骤，直到质心的位置变化小于制定的阈值或者达到最大迭代次数。

3.2 代码实现

1
2
3
4
5
6
7
8
9
try {
	Instances data = DataSource.read("src/main/resources/bank_data.arff");
    SimpleKMeans kMeans = new SimpleKMeans();
    kMeans.setNumClusters(6);
    kMeans.buildClusterer(data);
    System.out.println(kMeans);
} catch (Exception e) {
    e.printStackTrace();
}

首先通过DataSource读取数据集，创建SimpleKMeans对象，设置群数为6，随后导入数据，生成聚类器，最后打印聚类器信息

3.3 实验结果

设置群数为6，从分群结果可以分析出不同人群的特点。

image-20221013004241168

Prev
2023-08-09 14:53:19 # Big Data # weka
Next